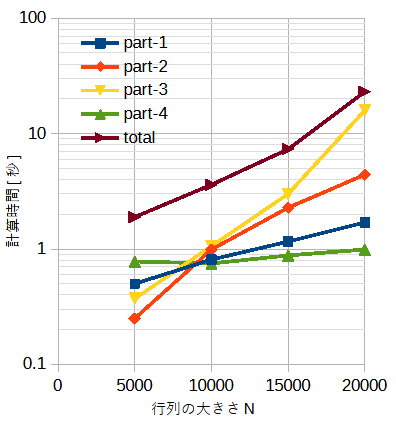
図9-4-1 Python版の計算時間(CPU:16スレッド、part-3:GPU使用、単精度)
計算時間の内訳は表9-4-1の通りです。
ここでNは線分要素数(=行列の大きさ)です。
| 内訳 | 内容 | 計算時間 |
|---|---|---|
| part-1 | 前処理、線分要素の作成 | ∝N2 |
| part-2 | インピーダンス行列の作成 | ∝N2 |
| part-3 | 連立一次方程式の求解 | ∝N3 |
| part-4 | 後処理 | ∝N |
計算の高速化のためにpart-1,part-2,part-3にNumbaを使用しています。
計算の主要部であるpart-3についてはCuPyを用いてGPUで高速に計算することもできます。
また、単精度と倍精度を選択することができます。
図9-4-1にベンチマークN=5000~20000の計算時間の内訳を示します。
part-3ではGPUを使用しています。
問題のサイズが大きくなるとpart-3の計算時間が最も大きくなります。

図9-4-1 Python版の計算時間(CPU:16スレッド、part-3:GPU使用、単精度)
図9-4-2に計算条件と計算時間の関係を示します。
計算の主要部であるpart-3のみの計算時間です。
CPUとGPU、単精度と倍精度を変えています。CPUは16スレッドです。
図からGPUで単精度で計算するとき他のケースより大幅に速いことがわかります。
GPUの倍精度が遅いのはハードウェアの制限の影響が考えられます。
またN=20000のときはメモリー不足で計算できません。
CPUでは単精度の計算時間は倍精度の約半分です。
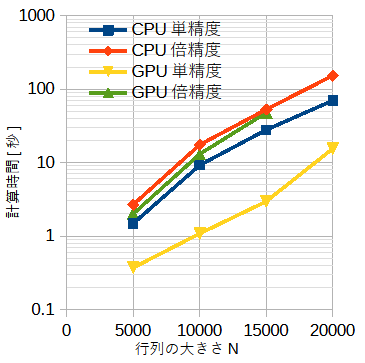
図9-4-2 Python版の計算時間(part-3のみ)