図2-2-1 直接波
(1) 直接波の定義
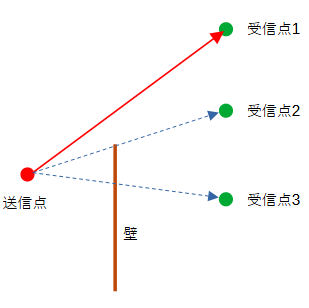
直接波とは、送信点から受信点までの間に障害物（壁）が存在せず直接伝わる波です。
図2-2-1において受信点1には直接波が到達し、
受信点3には途中に壁が存在するので直接波が到達しません。
受信点2はその境界ですが、ここでは直接波は到達しないものとみなし、
次節の回折波として扱います。
なお、2点間が見通し内であることをLOS(Line Of Sight)、
見通し外であることをNLOS(Non LOS)と呼びます。
図2-2-1 直接波
(2) 直接波の判定条件
OpenRTMでは物体は三角形の集合として扱います。
2点間が見通し内である否かの判定法は以下のようになります。
図2-2-2のように2点(ra,rb)
を結ぶ線分と3角形(r1,r2,r3)を考えます。
交点を2通りで表現すると、
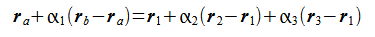(2-2-1)
となり、これを成分に分けると、
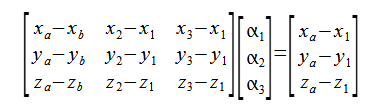(2-2-2)
となります。これを解いて、
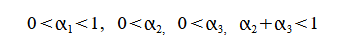(2-2-3)
のとき衝突します。
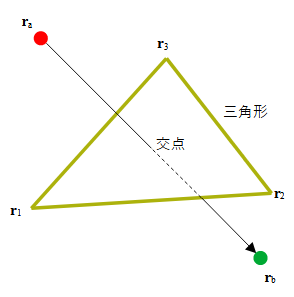
図2-2-2 線分abと三角形123の交差
(1) 反射波の判定条件
反射波が壁に当たって反射するときの反射点は、
受信点の壁による鏡像点と送信点との交点になります。
反射波が成立するためには、
送信点-反射点-受信点が見通し内であることが必要です。
ただし、図2-2-3の右のように反射点に別の壁が交わっている可能性があります。
この場合、上の判定だけでは左右のケースを区別することができません。
従って、反射点から送信点と受信点方向にごくわずかに移動した点1と点2をとり、
送信点-点1-点2-受信点が見通し内であるか調べます。
本来の反射波が存在する左のケースではすべて見通し内であり、
反射波が存在しない右のケースでは点1-点2間は見通し外になります。
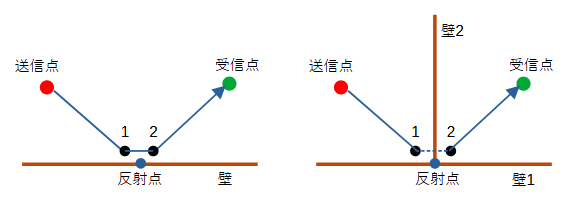
図2-2-3 反射波の判定方法（左：反射波あり、右：反射波なし）
(2) 鏡像点の計算
点Pの三角形による鏡像点P'は次式で計算されます。
ここで頂点1は三角形内の点であればなんでも構いません。
{}内が点Pと三角形との距離であることから確認できます。
また法線ベクトルの符号によらないので三角形の表裏を考える必要はありません。
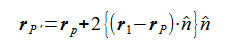(2-2-4)
(1) 回折波の定義
回折波とは、壁の辺（稜線、エッジ）を回り込む波です。
見通し外にも電波が到達します。
電波が波動であるために発生する現象です。
OpenRTMでは1回回折する波のみを考えます。
図2-2-4に回折波の3ケースを示します。
送信点1-受信点1には回折波が存在します。
送信点2-受信点2にも回折波が存在するとみなします。
送信点3-受信点3には直接波が存在するので回折波はないものとします。
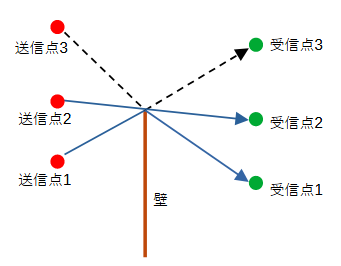
図2-2-4 1回回折波
(2) 回折波の判定条件
回折波が存在するためには、
送信点と回折点および回折点と受信点が見通し内であることが必要です。
通常は図2-2-5の左図ように回折点（図中の青丸）のわずかに外側に点1を考え、
送信点-点1-受信点が見通し内であるかどうか判定します。
しかしの右図のように回折点が複数の壁の境界にあるときは、
本来回折波は存在しませんが、上記の判定法では特殊なケースで回折波が発生します。
これを避けるために回折点の周囲のごく近傍に相対する2個の点を取り、
送信点-点1-受信点と送信点-点2-受信点の少なくとも一つが見通し内であるとき、
回折波が存在すると考えます。
この判定法により、回折波が存在する中図のケースと、
回折波が存在しない右図のケースを区別することができます。
ただし、回折波の計算は時間がかかります。
多くの場合、左図の簡易判定法によって約半分の計算時間でほぼ妥当な結果を得ることができます。
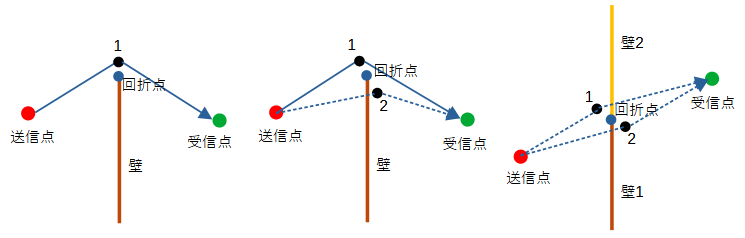
図2-2-5 回折波の判定法（左：回折波あり（簡易判定法）、中：回折波あり、右：回折波なし）
(3) 回折波の大きさ
回折波の大きさは楔モデルにより計算します。
図2-2-6のように、送信点1から受信点2へ稜線34を超える回折波が到達するものとします。
楔モデルでは回折波の大きさは稜線から送受信点を結ぶ線分までの最短距離PQで決まります。
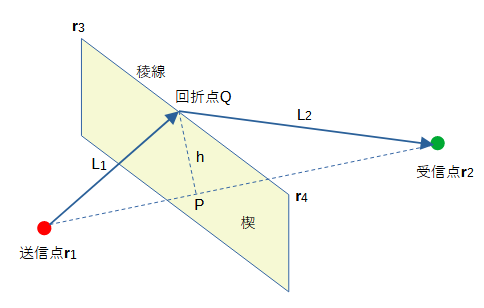
図2-2-6 回折波の楔モデル
送信点と受信点を結ぶ線分上の点をP、稜線上の点をQとすると、
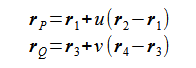(2-2-5)
となり、PQ間の距離の2乗は
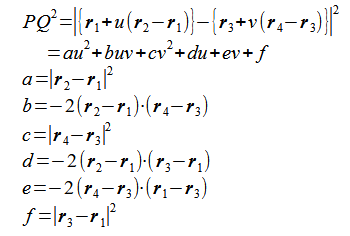(2-2-6)
となります。u,vに関する2次形式(2-2-6)を変形すると、
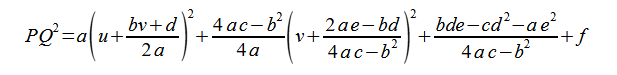(2-2-7)
となり、式(2-2-6)から
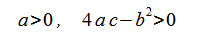(2-2-8)
であるから、式(2-2-7)の平方根は、
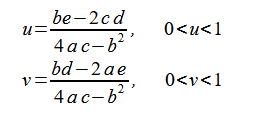(2-2-9)
のとき、最小値
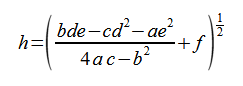(2-2-10)
をとります。
以上で求めた最短距離hから、回折波の大きさは次式で計算されます[2]。
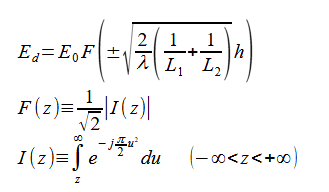(2-2-11)
ここで、E0は回折因子を除いた電界の強さ、
L1は送信点と回折点の距離、L2は回折点と受信点の距離であり、
符号は送受信間が見通し外のとき正、見通し内のとき負を取ります。
ただし、ここでは見通し内は考えません。
式(2-2-11)の回折因子Fは楔の角度と材質、および偏波に無関係な近似式です。
式(2-2-11)の第2式はz=-∞,0,+∞のときF(z)=1,0.5,0になります。
式(2-2-11)の第3式の計算には以下の近似式を用います[3]。
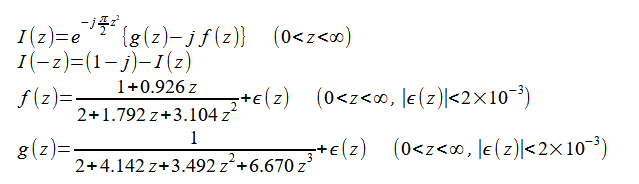(2-2-12)
なお、式(2-2-12)に代わる近似式として以下の二つがあります[2]。
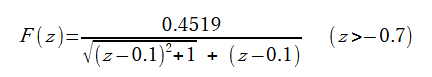(2-2-13)
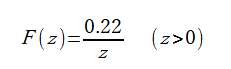(2-2-14)
図2-2-7に三つの式を比較します。
式(2-2-13)はz>-0.7で式(2-2-12)とよく一致しています。
式(2-2-14)は簡易な式ですがz>1で式(2-2-12)とよく一致しています。
式(2-2-11)(2-2-14)から回折波の大きさは周波数の1/2乗に反比例することがわかります。
従って周波数が2倍になると3dB小さくなります。
なお、OpenRTMは見通し内の回折波を考えないので図2-2-7のz>0のみを使用します
（z<0では0dBと考えることができます）。
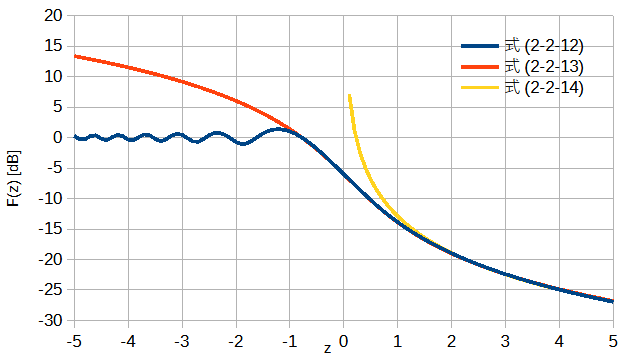
図2-2-7 回折因子
透過波とは壁を通過する波です。
壁に囲まれた送信点のない部屋における電界の強さを評価するために使用します。
OpenRTMでは一つの壁を通過するもののみを考えます（一回透過波）。
二回以上の透過波や、透過波+反射波などは考えません。
透過波の位置関係は図2-2-8のようになります。
透過波の伝搬経路は送信点を受信点を結ぶ直線です。
透過波が存在するためには、送信点を受信点を結ぶ直線が壁と交差し、
送信点と透過点および透過点と受信点が見通し内(LOS)であることが必要です。
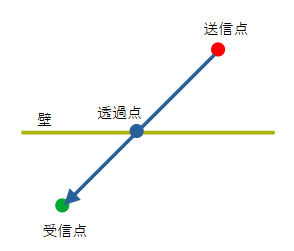
図2-2-8 1回透過波