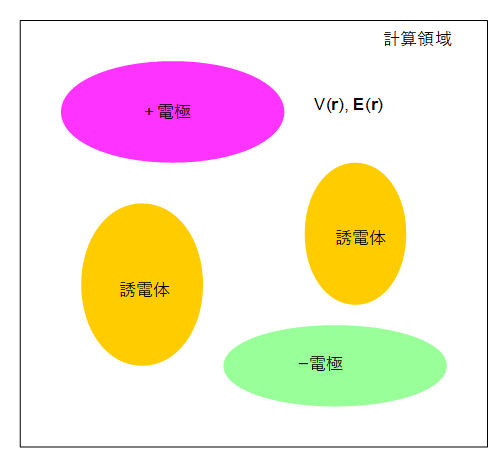
図2-1-1 静電界の計算モデル
図2-1-1のように、3次元の計算領域の中に2個以上の電圧の異なる電極が存在するとき電圧分布が発生します。
さらに誘電体があると電圧分布に影響を与えます。
OpenSTFはこのような系における電圧分布と電界分布を計算するものです。[1][2]

図2-1-1 静電界の計算モデル
Maxwell方程式から次式が得られます。
ここでDは電束密度です。なお、点電荷は考えません。
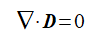 (2-1-1)
(2-1-1)
構成方程式は以下のようになります。
ここでEは電界、εは誘電率です。
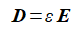 (2-1-2)
(2-1-2)
誘電率は次式のように表されます。
ここでε0=8.854e-12[F/m]は真空の誘電率、εrは比誘電率です。
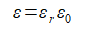 (2-1-3)
(2-1-3)
電界と電圧の関係式は以下のようになります。
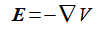 (2-1-4)
(2-1-4)
式(2-1-2),(2-1-3),(2-1-4)を式(2-1-1)に代入すると以下の式が得られます。
これが基本となる方程式です。
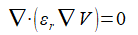 (2-1-5)
(2-1-5)
計算領域を多数のメッシュに分割し、
節点(i,j,k) (i=0,...,Nx, j=0,...,Ny, k=0,...,Nz) の座標を
(xi, yj, zk)と表します。
節点の総数はN=(Nx+1)*(Ny+1)*(Nz+1)個です。
式(2-1-5)を差分法によって節点(i,j,k)で離散化すると次式が得られます。
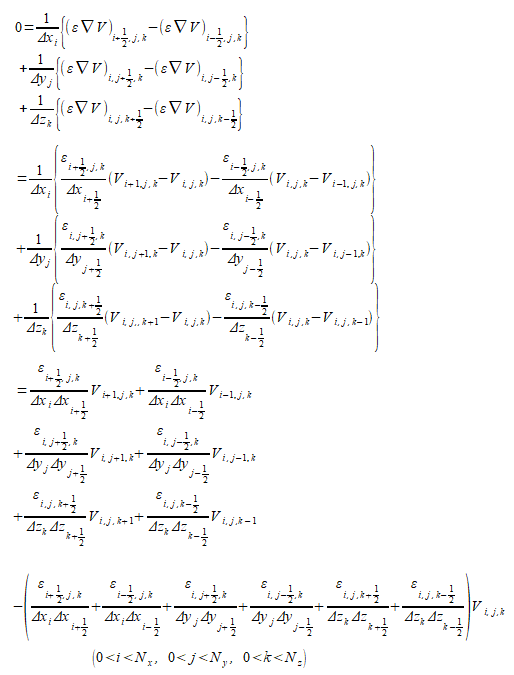 (2-1-6)
(2-1-6)
ここでセルサイズの計算式は以下の通りです。
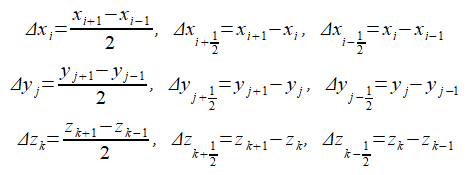 (2-1-7)
(2-1-7)
計算領域の境界における境界条件は以下のNeumann条件を考えます。
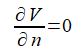 (2-1-8)
(2-1-8)
式(2-1-8)を離散化すると以下のようになります。
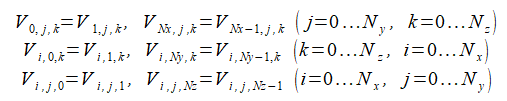 (2-1-9)
(2-1-9)
電極の上では電圧は既知量となります。
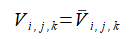 ((i,j,k) ∈ 電極) (2-1-10)
((i,j,k) ∈ 電極) (2-1-10)