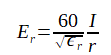5.10 同軸線路

同軸線路の固有モードと特性インピーダンスを計算します。
リスト5-10-1に入力データを示します。
図5-10-1に形状出力図を示します。 2次元モデルとなり、外導体、誘電体、内導体から成ります。
図5-10-2に電界の線上分布図を示します。
図5-10-3に電界の面上分布図を示します。電界分布は同心円のTEMモードになります。
同軸線路内部の電界は次式で表されます。

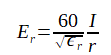(5-10-1)

これから電界は動径rに反比例することがわかります。 Nx=Ny=200とNx=Ny=400の2ケースで電界と動径の積をプロットすると図5-10-4のようにほぼ一定値となります。 後者のセルサイズは前者の半分なので厳密解は図のように外挿によりEr*r=0.72Vと推定されます。
このEr*rから式(5-10-2)によって電流Iが求められ、 それを式(5-10-3)に代入すると特性インピーダンスは50.1Ωとなります。(V=1)
一方特性インピーダンスの公式(5-10-4)からは50.0Ωとなり両者は近い値になります。

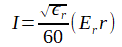(5-10-2)
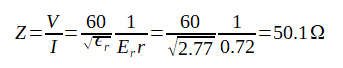(5-10-3)
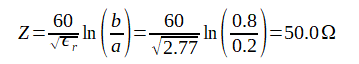(5-10-4)

リスト5-10-1 同軸線路(coax.ost)

OpenSTF 1 3
title = 同軸線路
xmesh = -1 400 1
ymesh = -1 400 1
zmesh = 0 2 0
volt = 1 
volt = 0 
epsr = 2.77 
geometry = 1 1 13 -1 1 -1 1 0 0 外導体
geometry = 2 1 13 -0.8 0.8 -0.8 0.8 0 0 誘電体
geometry = 1 2 13 -0.2 0.2 -0.2 0.2 0 0 内導体
solver = 1.98 2000 50 1e-6
plot1d = V X 0 0
plot1d = E X 0 0
1ddb = 0
1dlog = 1
plot2d = V Z 0
plot2d = E Z 0
2dfigure = 1 0
2ddb = 0
2dobject = 1 1
2dlog = 1
window2d = 750 500 15
window3d = 500 500 60 30
end

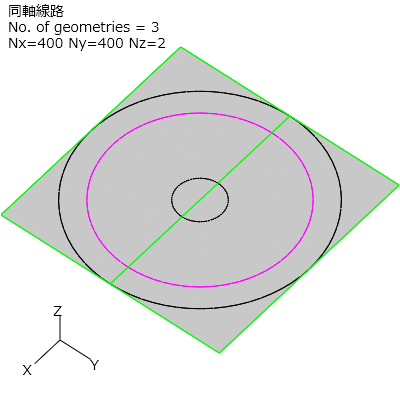
図5-10-1 形状出力図

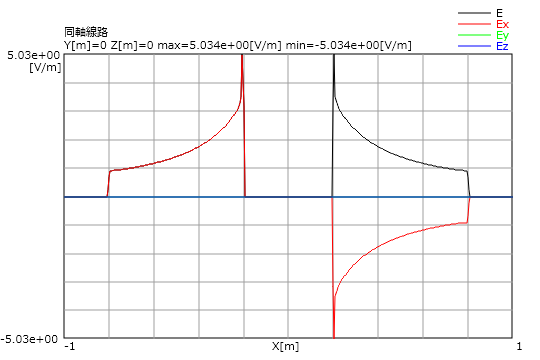
図5-10-2 電界線上分布図

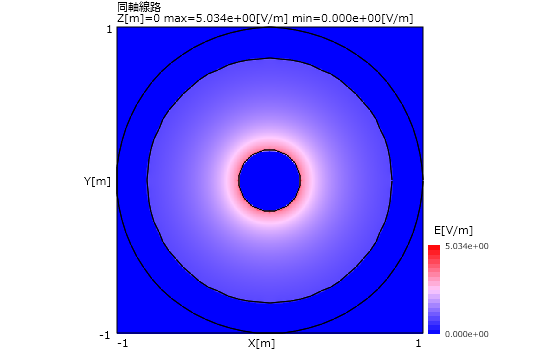
図5-10-3 電界面上分布図

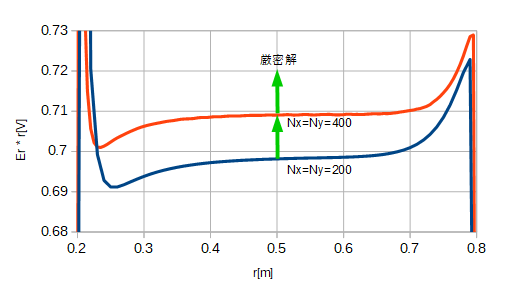
図5-10-4 Er * rとrの関係