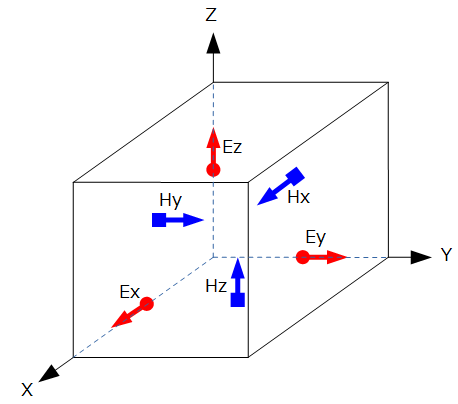
図2-2-1 Yee格子
差分法の空間格子としてはFDTD法と同じく図2-2-1のYee格子を考えます。

図2-2-1 Yee格子
以下では格子の1単位(直方体)をセルと呼びます。
計算領域のX/Y/Z方向のセル数をNx/Ny/Nzとします。
セル分割は不均一分割にも対応し、節点(セルの頂点)の座標を、
xi (i=0,...,Nx), yj (j=0,...,Ny), zk (k=0,...,Nz)
と表します。
電界の各成分は式(2-2-1)のように表示されます。
ここでセルの中心を半整数で表しています。
電界のX成分のi、Y成分のj、Z成分のkが半整数になり、それ以外は整数になります。
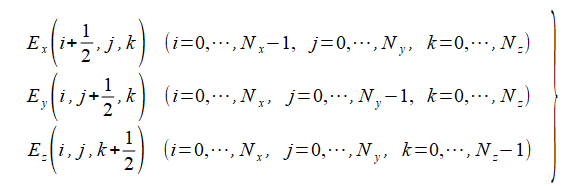 (2-2-1)
(2-2-1)
また離散化のための座標の差分を式(2-2-2)(2-2-3)のように定義します。
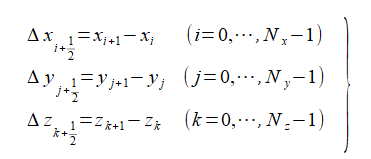 (2-2-2)
(2-2-2)
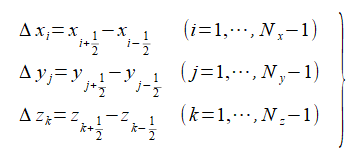 (2-2-3)
(2-2-3)