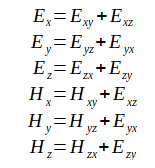2.7 PML吸収境界条件

PML(Perfectly Matched Layer)[5]では電磁界の各成分を次式のように分解します。

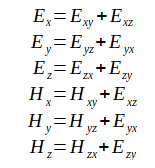(2-7-1)

各成分は次式を満たします。ここで 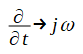を適用しています。

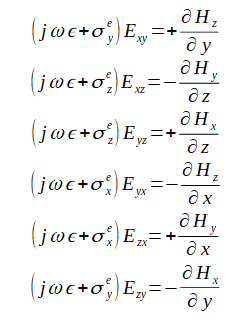(2-7-2)
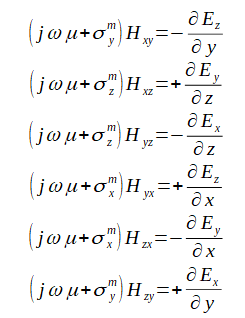(2-7-3)

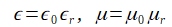はPML領域内の誘電率と透磁率の実部(一定値)であり、本来の計算領域の境界面の値を使用します。
また 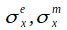はXの関数、 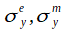はYの関数、 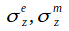はZの関数であり具体的な式は後で述べます。
次式のインピーダンス整合条件を仮定します。

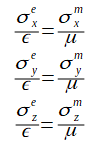(2-7-4)

次式で無次元の係数を定義します。

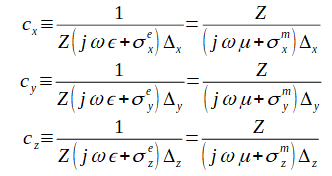(2-7-5)

ただし、 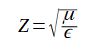です。

式(2-7-5)を式(2-7-2)(2-7-3)に代入すると次式になります。

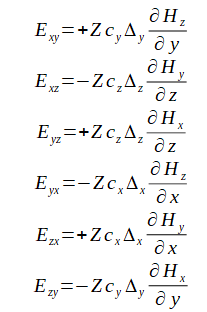(2-7-6)
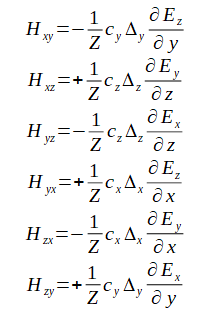(2-7-7)

式(2-7-6)(2-7-7)を式(2-7-1)に代入すると次式になります。

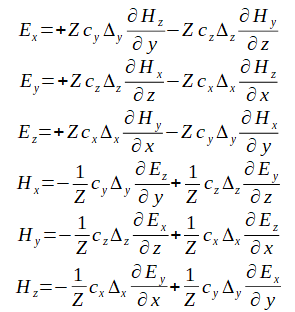(2-7-8)

式(2-7-8)から磁界Hを消去すると次式が得られます。

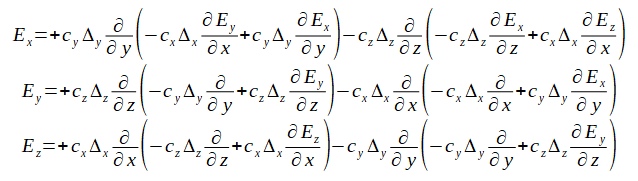(2-7-9)

式(2-7-9)のX成分を離散化すると次式が得られます。

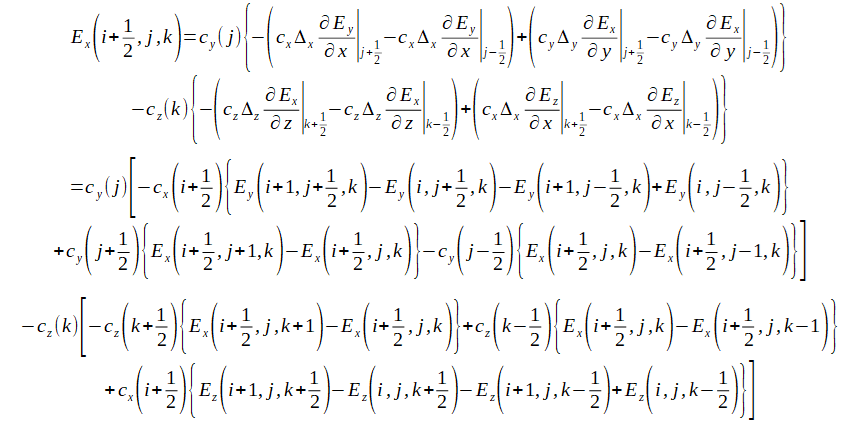(2-7-10)

式(2-7-10)を電界の各項について整理すると次式が得られます。 図2-3-1と同じく13点差分になります。

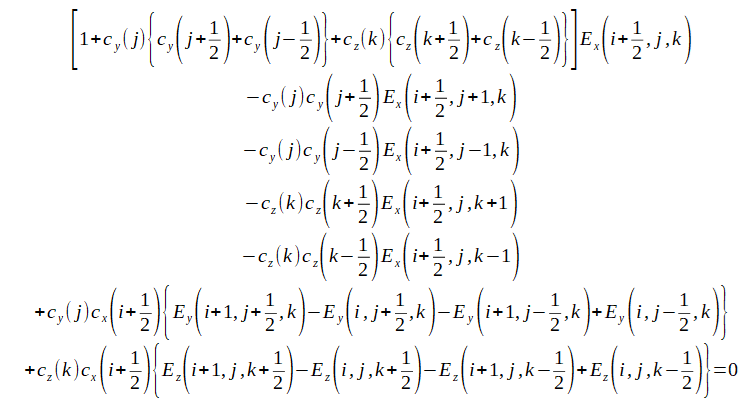(2-7-11)

Y,Z成分についてはX,Y,Zを巡回させて次式が得られます。

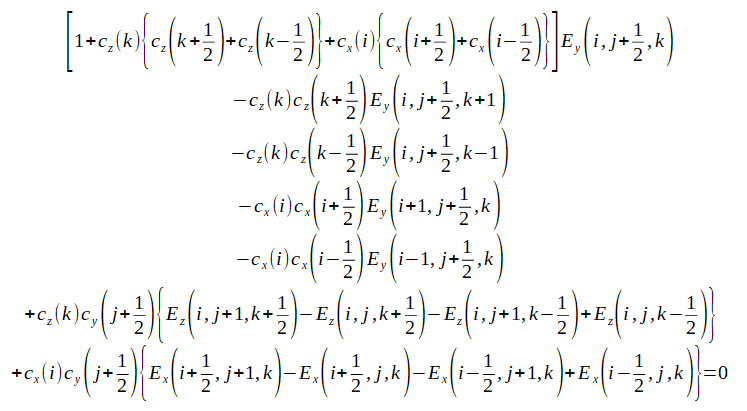(2-7-12)
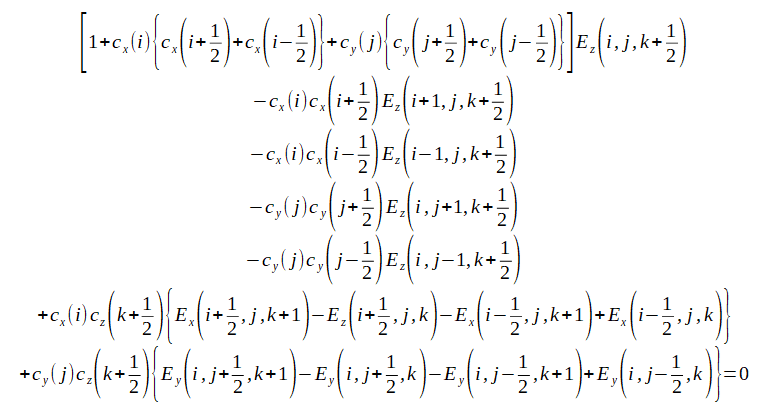(2-7-13)

なお、PML領域の外境界面では電界=0とします。

式(2-7-5)の導電率は次式とします。ここでLはPMLの層数、Mは次数です。

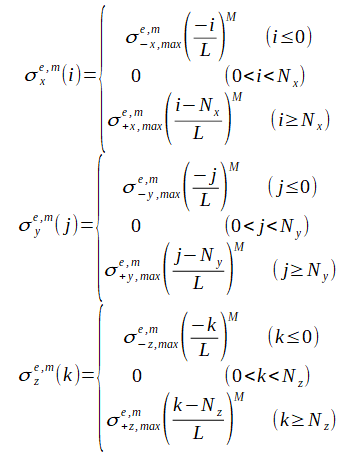(2-7-14)
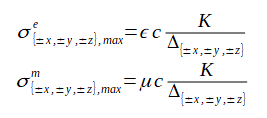(2-7-15)
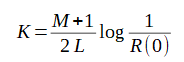(2-7-16)

ここでR(0)は垂直入射の反射係数であり、KはPMLのパラメータで決まる無次元の正の数です。 L,M,R(0)はユーザーが指定するパラメーターです。
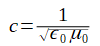は真空中の光速、 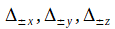は±X,±Y,±Z境界のPML層のセルサイズ 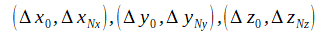です。
以上から式(2-7-5)は次式で計算されます。

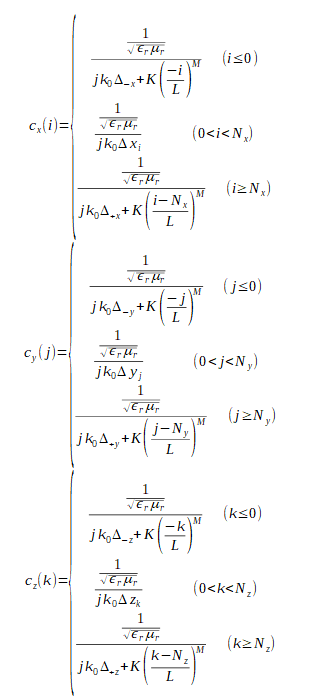(2-7-17)