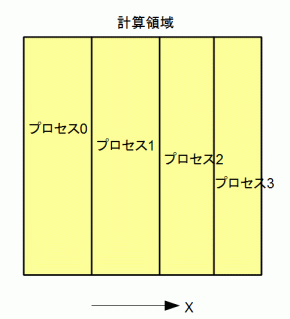
図3-4-1 領域分割
MPIでは計算領域をプロセスの数で分割します。
本プログラムはX方向に分割します。
図3-4-1は計算領域をX方向に4分割したものです。
X方向のセル数Nxがプロセス数Npの倍数でないときはなるべく不均一性が小さくなるように分割します。
各プロセスの必要メモリーはプロセス数分の1になります。
これにより計算ノードの数を増やせばそれに比例して計算できる問題サイズの上限が大きくなります。

図3-4-1 領域分割
MPIでは行列・ベクトル積の計算の前に計算領域の境界で隣のプロセスとの通信が必要になります。
プロセスPは領域境界より左の成分を所有し、プロセスP+1は領域境界上とその右の成分を所有します。
通信する成分は図3-4-1に矢印で示した成分です。
このうち、赤い成分はプロセスPからプロセスP+1の方向に通信し、
青い成分はプロセスP+1からプロセスPの方向に通信します。
これによりプロセスP,P+1ともに自分の所有する成分を更新することができます。
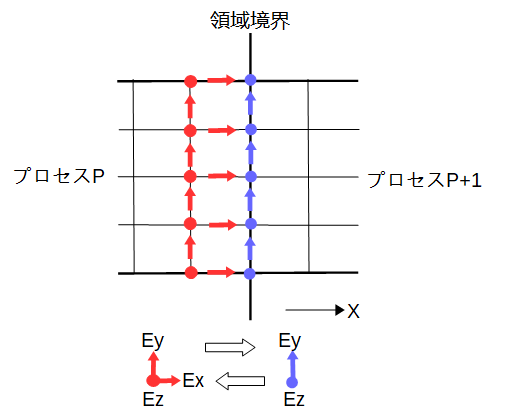
図3-4-2 電界の通信
リスト3-4-1にMPIにより電界を通信するプログラムを示します。
アドレスと通信量は予め計算し、バッファーも予め確保しています。
リスト3-4-1 MPIによる電界の通信
void comm_boundary(d_complex_t *v)
{
#ifdef MPI
MPI_Status status;
const int tag = 0;
// -X direction
if (commRank > 0) {
// copy to send buffer
memcpy(Sendcomplex_m, &v[Send0_m], Sendcount_m * sizeof(d_complex_t));
for (int64_t n = 0; n < Sendcount_m; n++) {
Sendbuf_m[(2 * n) + 0] = Sendcomplex_m[n].r;
Sendbuf_m[(2 * n) + 1] = Sendcomplex_m[n].i;
}
// MPI
int dst = commRank - 1;
MPI_Sendrecv(Sendbuf_m, 2 * Sendcount_m, MPI_DOUBLE, dst, tag,
Recvbuf_m, 2 * Recvcount_m, MPI_DOUBLE, dst, tag, MPI_COMM_WORLD, &status);
// copy from recv buffer
for (int64_t n = 0; n < Recvcount_m; n++) {
Recvcomplex_m[n].r = Recvbuf_m[(2 * n) + 0];
Recvcomplex_m[n].i = Recvbuf_m[(2 * n) + 1];
}
memcpy(&v[Recv0_m], Recvcomplex_m, Recvcount_m * sizeof(d_complex_t));
}
// +X direction
if (commRank < commSize - 1) {
// copy to send buffer
memcpy(Sendcomplex_p, &v[Send0_p], Sendcount_p * sizeof(d_complex_t));
for (int64_t n = 0; n < Sendcount_p; n++) {
Sendbuf_p[(2 * n) + 0] = Sendcomplex_p[n].r;
Sendbuf_p[(2 * n) + 1] = Sendcomplex_p[n].i;
}
// MPI
int dst = commRank + 1;
MPI_Sendrecv(Sendbuf_p, 2 * Sendcount_p, MPI_DOUBLE, dst, tag,
Recvbuf_p, 2 * Recvcount_p, MPI_DOUBLE, dst, tag, MPI_COMM_WORLD, &status);
// copy from recv buffer
for (int64_t n = 0; n < Recvcount_p; n++) {
Recvcomplex_p[n].r = Recvbuf_p[(2 * n) + 0];
Recvcomplex_p[n].i = Recvbuf_p[(2 * n) + 1];
}
memcpy(&v[Recv0_p], Recvcomplex_p, Recvcount_p * sizeof(d_complex_t));
}
#endif
}
表3-4-1と図3-4-3にプロセス数と計算時間の関係を示します。
プロセス数が少ないときはmatrixモードの方が速いですが、
プロセス数が多いときはnomatrixモードの方が速くなります。
ただし、両者の差は小さいので使用メモリーの少ないnomatrixモードを推奨します。
またプロセス数は物理コア数(=8)と論理コア数(=16)の差は小さいのでどちらでもかまいません。
以上の性質はOpenMPとMPIで同じあり、計算時間もほぼ同じです。
従ってCPUの高速化はOpenMPとMPIのどちらを使用してもかまいません。
| プロセス数 | benchmark100 | benchmark200 | ||
|---|---|---|---|---|
| nomatrix | matrix | nomatrix | matrix | |
| 1 | 142秒 (1.0) | 86秒 (1.0) | 1123秒 (1.0) | 688秒 (1.0) |
| 2 | 77秒 (1.8) | 50秒 (1.7) | 830秒 (1.4) | 565秒 (1.2) |
| 4 | 56秒 (2.5) | 39秒 (2.2) | 474秒 (2.4) | 344秒 (2.0) |
| 8 | 39秒 (3.6) | 38秒 (2.3) | 319秒 (3.5) | 286秒 (2.4) |
| 16 | 42秒 (3.4) | 47秒 (1.8) | 268秒 (4.2) | 328秒 (2.1) |
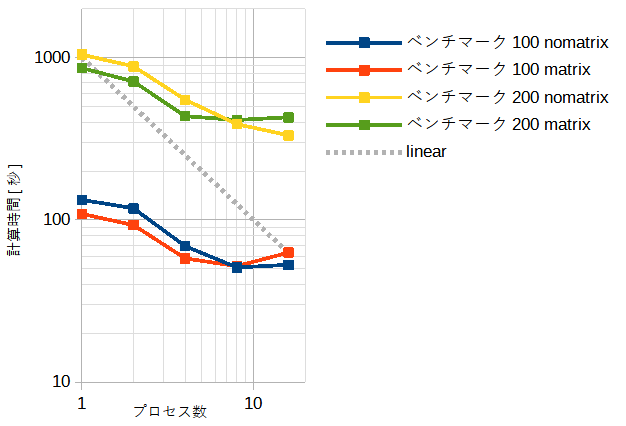
図3-4-3 MPIの計算時間(CPU)
OpenTHFDはOpenMPとMPIで並列化されているのでそれらを併用することができます。
CPUのコア数をOpenMPのスレッド数とMPIのプロセス数に分割します。
表3-4-2は8コアのCPUの結果です。
どのように分割しても計算時間はほぼ同じです。
| MPIプロセス数 | OpenMPスレッド数 | ベンチマーク100 nomatrix |
|---|---|---|
| 1 | 8 | 36秒 |
| 2 | 4 | 36秒 |
| 4 | 2 | 36秒 |
| 8 | 1 | 39秒 |