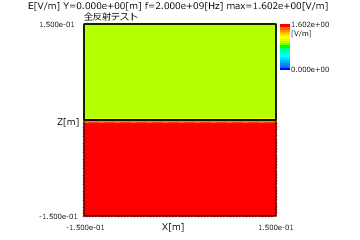
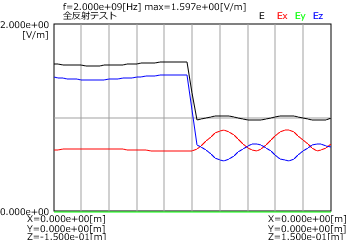
図1 通常反射の場合(P偏波、入射角=40度)
2.5.4で述べた半領域に平面波が入射するモデルをテストします。
ここでは境界面のみでそれ以外に物体が何もないモデルを考えます。
このとき電磁界は法線方向のみの関数になり、横方向に一様になります。
■入力データ:
total_reflection_1d.oth,
total_reflection_2d.oth,
total_reflection_3d.oth
比誘電率εr=2の媒質からεr=1の媒質に入射するときは、
入射角が臨界角=sin-1(1/√2)=45度を越えると全反射になります。
図1に通常反射の(P偏波、入射角=40度)の電界分布を示します。
入射側は入射波と反射波で定在波ができ、透過側は振幅一定の透過波が伝搬します。


図1 通常反射の場合(P偏波、入射角=40度)
図2と図3にP偏波とS偏波の全反射の(入射角=50度)の電界分布(上)と磁界分布(下)を示します。
これから全反射では透過側では電界と磁界が指数関数で減衰することがわかります。
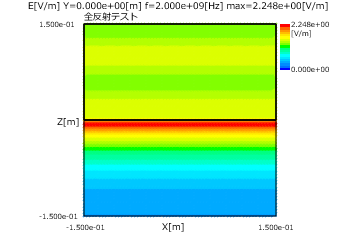
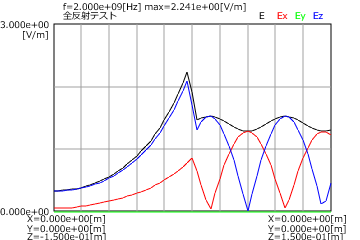
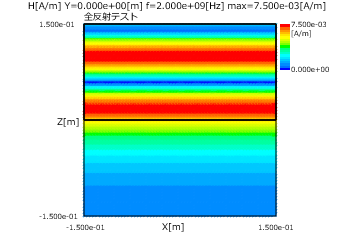
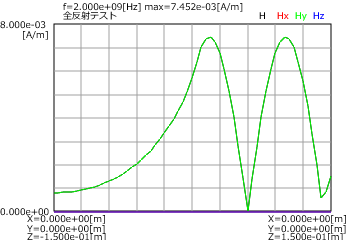
図2 全反射の場合(P偏波、入射角=50度、上:電界、下:磁界)
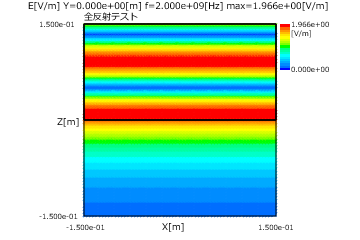
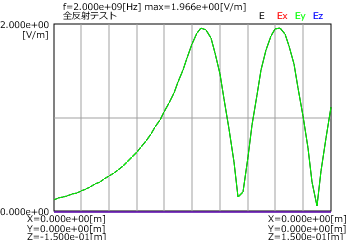
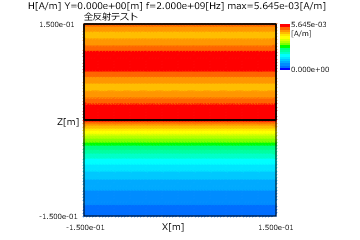
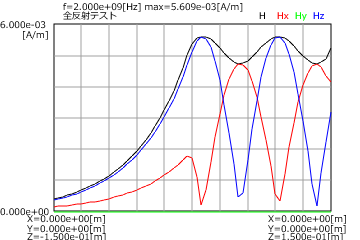
図3 全反射の場合(S偏波、入射角=50度、上:電界、下:磁界)
本モデルは1次元モデルなので1次元,2次元,3次元の入力データで同じ計算結果になります。
なおX方向とY方向に周期境界条件を設定しています。
境界面周辺に構造物を置いてその反射波と透過波を見るには2次元または3次元モデルを使用します。
■入力データ:
brewster_1d.oth,
brewster_2d.oth,
brewster_3d.oth
P偏波で比誘電率εr=1の媒質からεr=3の媒質に入射するときは、
入射角がtan-1(√3)=60度のときBrewster角になり反射係数がゼロになります。
図4に縦方向の電界と磁界を示します。
反射係数がゼロであるために反射側(図の右半分)でも電磁界が一定になっています。
本モデルは1次元モデルなので1次元,2次元,3次元の入力データで同じ計算結果になります。
なお、本ケースでは周期境界条件の有無で結果はあまり変わりませんが、
周期境界条件は収束を速くする効果があります。
電磁界の境界条件により電界と磁界の接線成分は連続になり、
電束密度(D=εE)と磁束密度(B=μH)の法線成分は連続になります。
図から電界の接線成分Exと磁界の接線成分Hyが連続になり、
電界の法線成分Ezが誘電率の比で不連続になることが確認できます。
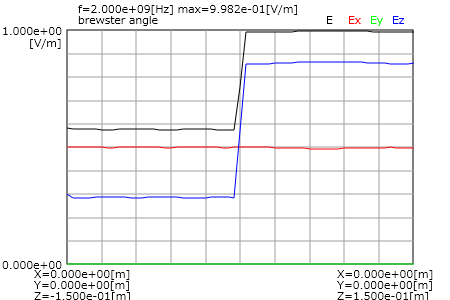
(a)電界分布
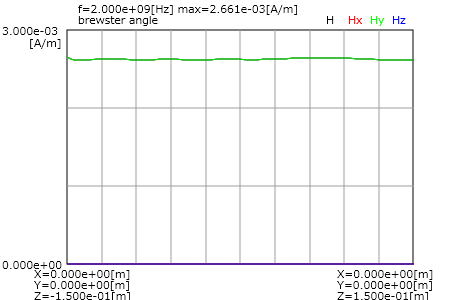
(b)磁界分布
図4 Brewster角
■入力データ: P45deg.oth
P偏波45度入射時の電界分布を図5に示します。
反射側(図の右半分)の電界のX成分とZ成分は定在波になりますが、
その合成電界は場所によらず一定になることがわかります。
なお、本ケースでは周期境界条件の有無で結果はあまり変わりませんが、
周期境界条件は収束を速くする効果があります。
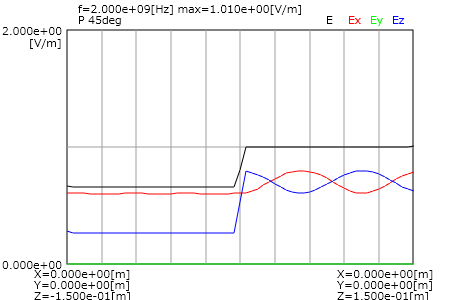
図5 P偏波45度入射