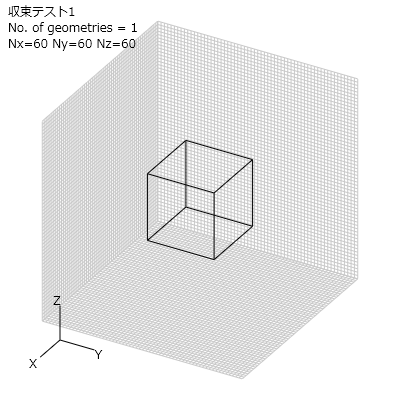
図1 収束性テストの計算モデル1
メッシュ分割および吸収境界条件と収束状況の関係について調べます。
計算モデルはすべて一辺1λの完全導体の立方体に平面波が入射するモデルです。
PMLの条件はすべてL=5, M=2, R0=1e-5とします。
■入力データ:
convergence1.oth,
convergence2.oth,
convergence3.oth
(1) 立方体均一メッシュ
図1の立方体の均一メッシュを計算します。
図2より良好な収束性であり、PMLはMurの約2倍の反復回数を必要とします。

図1 収束性テストの計算モデル1
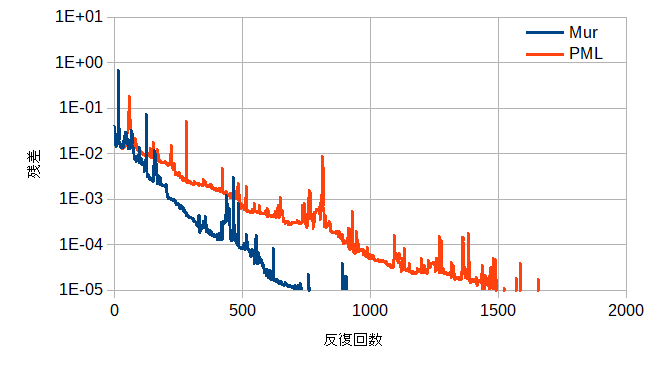
図2 吸収境界条件と収束状況
(2) 直方体メッシュ
図3のXYZ各方向に均一分割でセルサイズが異なる直方体のモデルを計算します。
辺の比(アスペクト比)は最大75/45=1.666です。
図4よりPMLの収束状況が悪くなります。
これからPMLのときはアスペクト比を大きくしないことが必要です。
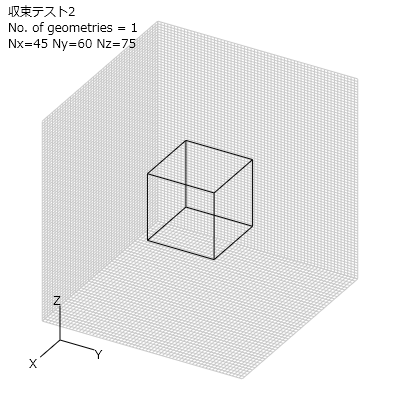
図3 収束性テストの計算モデル2
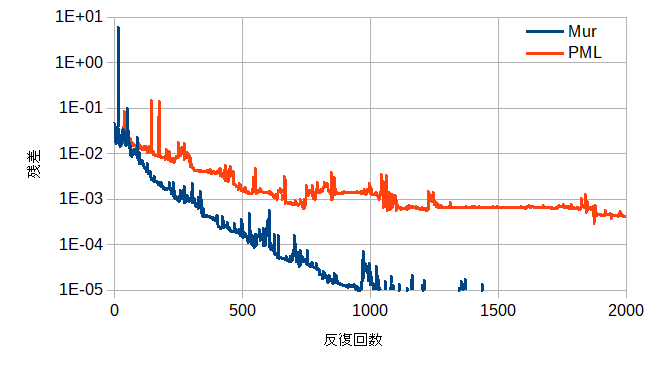
図4 吸収境界条件と収束状況
(3) 不均一メッシュ
図5のXYZ各方向で不均一なメッシュのモデルを計算します。
セルサイズの比は1:2です。
図6よりMur/PMLともに収束状況が悪くなります。
これからメッシュの不均一度は1:2以下にしたほうがよいことがわかります。
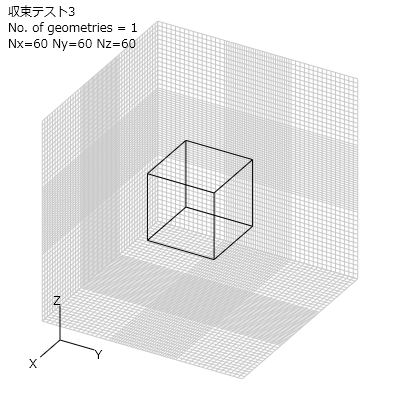
図5 収束性テストの計算モデル3
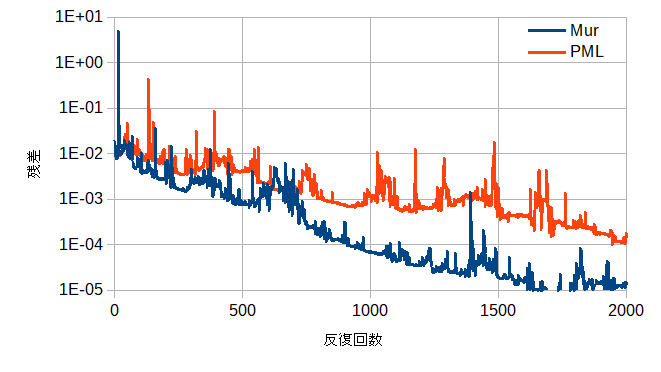
図6 吸収境界条件と収束状況