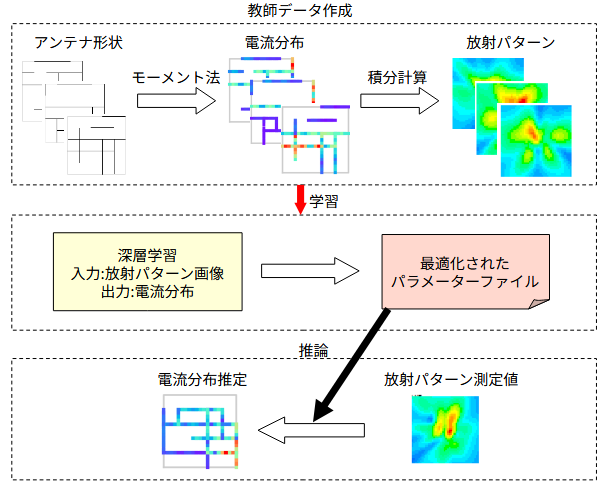
図2-1に処理の流れを示します。
以下の三つの部分から成ります。

図2-2に40個のアンテナ形状を示します。
Ny=Nz=20のメッシュ領域をとり、
その中に1本から20本のランダムな本数の完全導体の線分を置きます。
線分の向きは縦横ランダムに半分ずつとし、
線分の始点と終点の位置はランダムとします。
線分の座標は4セルの倍数とします。
結果、約10%の線分がアンテナで占有されます。
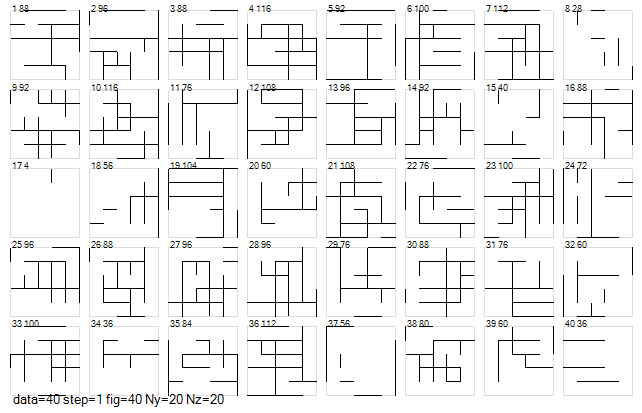
図2-3にモーメント法の計算モデルを示します。
物体はX=0面上にあるものとし、物体を導線の集合で表すワイヤグリッドモデルを採用します。
一つの線分(図の赤線)を給電点とします。
アンテナの存在する範囲の中心を原点とします。
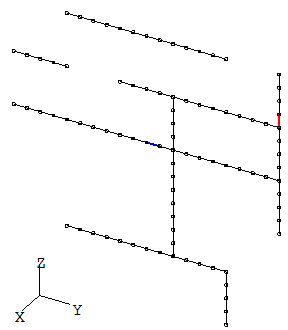
図2-4にモーメント法により電流分布を計算した結果を示します。
青→赤は電流の大きさを表します。
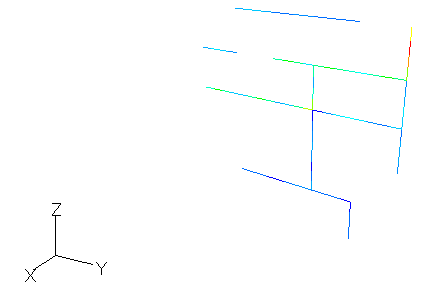
図2-5に全方向遠方放射パターンを示します。アンテナ形状も重ね書きしています。
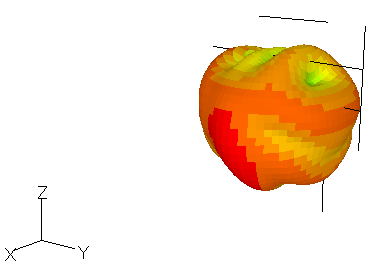
図2-6にX一定面の近傍電界分布を示します。アンテナ形状も重ね書きしています。
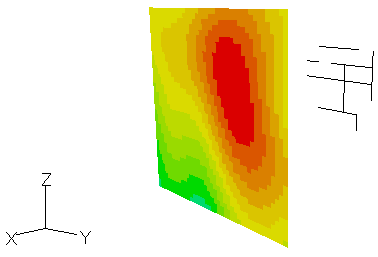
図2-6に電流分布の計算結果を示します。アンテナ形状は図2-2に対応しています。
図(a)はワイヤグリッド上の電流(複素数)そのままの絶対値です。
図(b)はワイヤグリッド上の電流をセル中心の電流IyとIz(複素数)に補間したのち、
絶対値I=√(|Iy|2+|Iz|2)をとったものです。
図の上の数値はデータ番号と電流最大値です。
補間のため図(b)の電流値は図(a)の約半分になります。
なお、学習に使用する電界分布はアンテナの有無に関係なく全線分の電流です。
アンテナの存在しない線分には電流値0を代入します。

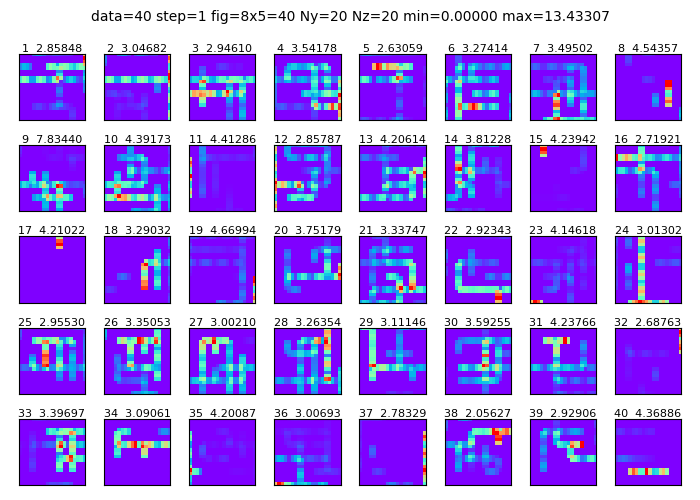
図2-7 電流分布の教師データ
図2-8に遠方界を示します。縦軸はθ、横軸φです。
遠方界は横波であるためにEθとEφの2成分の複素数であり、
その絶対値E=√(|Eθ|2+|Eφ|2)を表示しています。
アンテナ面をX面とした理由は遠方界を極座標で表したときに便利なためです。
図の上の数値はデータ番号と最大利得(単位V/m)です。
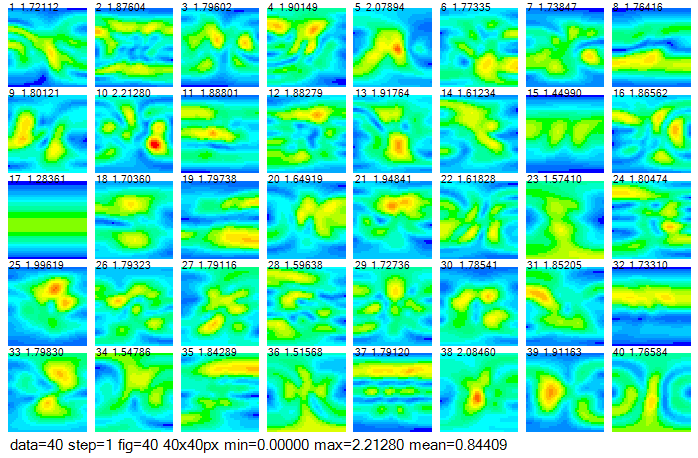
図2-9にX一定面の近傍界を示します。横軸はY方向、横軸はZ方向です。
E=√(|Ex|2+|Ey|2+|Ez|2) を表示しています。
図の上の数値はデータ番号と最大電界(単位V/m)です。
なお、磁界のときは電界と大きさを合わせるために自由空間の特性インピーダンス376.73Ωを掛けます。
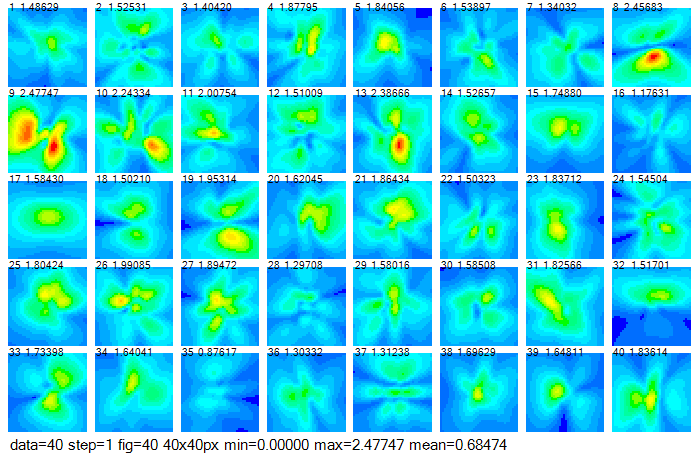
図2-8と図2-9を比べると遠方界分布と近傍界分布は似ていることがわかります。
近傍界の距離が遠くなるほど似てきます。ただし距離の不均一の影響は残ります。
なお、教師データとして使用する放射電界の成分についてはいろいろな組み合わせが考えられます。
前項の方法でアンテナ形状をランダムに変えて計算し、多数の教師データを作成します。
そのデータを用いて深層学習を行い、
遠方または近傍の放射パターンから電流分布を推定することを考えます。
以下では、ネットワークのの入力である放射パターンを"image"、
出力である電流分布を"label"と呼びます。
損失の計算式は式(2-1)の通りです。
総和nはデータに関するもの、総和sはメッシュの線分に関するものです。
総和mのとり方は以下の3通りを考えます。
(1) m=0 : 電流成分数M=1
(2) m=1,2 : 電流成分数M=2
(3) m=0,1,2 : 電流成分数M=3
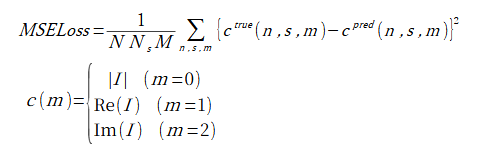 (2-1)
(2-1)
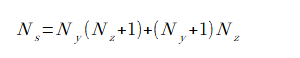 (2-2)
(2-2)
ここで、Nはデータ数、Nsはメッシュの線分数、Mは電流成分数(=1/2/3)、
ctrueとcpredは電流分布の正解(教師データ)と推定値です。
反復計算時に表示される"損失(loss)"は式(2-1)の平方根とします。
これは電流分布の推定誤差を表します。
なお、アンテナが存在しない場所では、ctrue=0であり、
cpredも0に近い値になります。
リスト2-1に学習部のソースコードを示します。
ユーザーの行う作業は以下の2点です。
リスト2-1 学習部のソースコード(PyTorch)
dataset設定 ※1
dataloader設定
model設定 ※2
criterion = nn.MSELoss() # 損失関数: MSE
optimizer = optim.Adam(model.parameters()) # 最適化関数: Adam
for epoch in range(num_epochs): # エポックに関するループ
for data, target in train_loader: # ミニバッチに関するループ
optimizer.zero_grad() # 勾配初期化
output = model(data) # 順伝搬
loss = criterion(output, target) # 損失計算
loss.backward() # 逆伝搬
optimizer.step() # 最適化関数更新
学習モデルには画像処理に適したCNN(畳み込みニューラルネットワーク)
の1種であるResNet[6][7]を使用します。
ここでは、ResNet18, ResNet34, ResNet50の3通りを考えます。
モデルを定義する方法は以下の通りです。
ゼロから(ランダムな初期値から)学習するには以下のいずれかになります。
model = models.resnet18(weights=None) model = models.resnet34(weights=None) model = models.resnet50(weights=None)最適化されたパラメーターからファインチューニングするには以下のいずれかになります。
model = models.resnet18(weights=models.ResNet18_Weights.DEFAULT) model = models.resnet34(weights=models.ResNet34_Weights.DEFAULT) model = models.resnet50(weights=models.ResNet50_Weights.DEFAULT)ここでは前者を「重みなし」、後者を「重みあり」と呼びます。
model.conv1 = nn.Conv2d(入力サイズ, 64, 7, stride=2, padding=3, bias=False) model.fc = nn.Linear(model.fc.in_features, 出力サイズ)入力サイズ = 放射電界成分数