特に断らない限り、モーメント法の計算条件は以下の通りです。
深層学習の計算条件は以下の通りです。
電流分布の成分数は式(2-1)のように3通りあります。
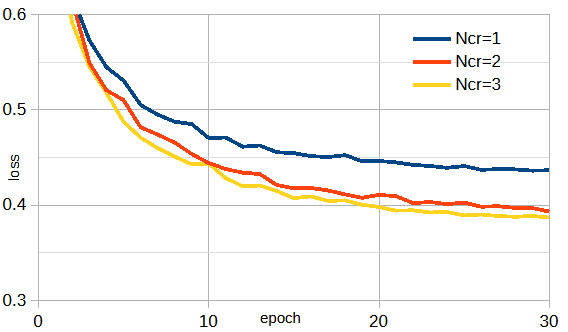
図3-1に各ケースの損失を示します。電流成分数=3が最も優れています。
以下では電流成分数=3とします。

図3-2に遠方界成分と損失の関係を示します。
図から、振幅のみでは電流分布は推定できないことがわかります。
また、遠方界成分数=4のとき損失が最も小さいことがわかります。
以下では、遠方界成分数=4
(Re(Eθ),Im(Eθ),Re(Eφ),Im(Eφ))とします。
なお、Eφの実部と虚部のときがEθの実部と虚部のときより有意に劣る理由は不明です。
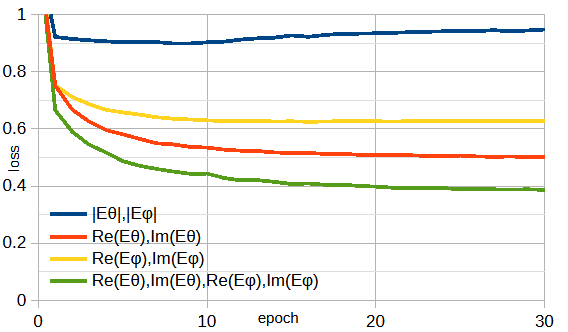
図3-3にResNet18/34/50の重みあり/なしの損失を示します。
ResNet18/34/50のepochあたりの計算時間は6/10/14秒です。
以下では、性能と計算時間を考慮して ResNet34 重みなし を使用します。
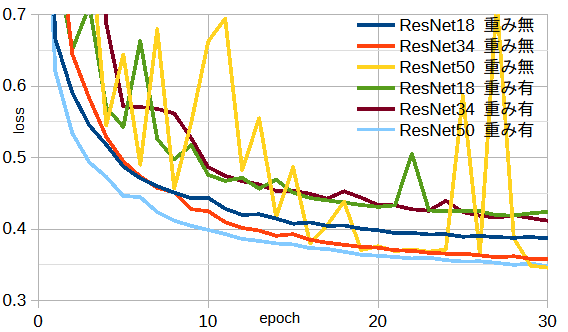
図3-4に遠方界の角度分割数(Nθ,Nφ)を変えたときの損失を示します。
分割数を大きくすると損失が小さくなり、Nθ=Nφ=56,64は同等です。
なお、アンテナが大きくなると遠方界の変動が大きくなり大きめの角度分割数が必要になります。
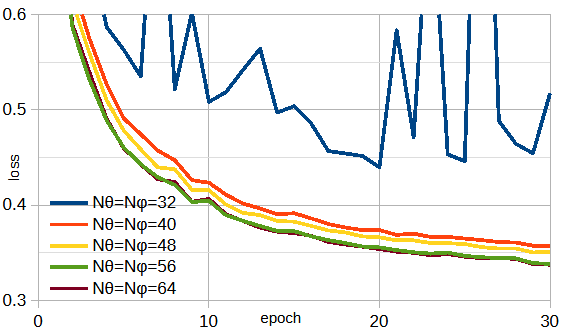
図3-5に遠方界の角度範囲を変えたときの損失を示します。
図から、角度範囲Δθ=Δφ=135度までは大きな違いはなく、
これより狭くなると急激に損失が大きくなることがわかります。
なお、アンテナが大きくなると遠方界の変動が大きくなり小さめの角度範囲で十分になります。
ただし、精度よく学習するためには一定以上の角度分割数(画素数)が必要です。
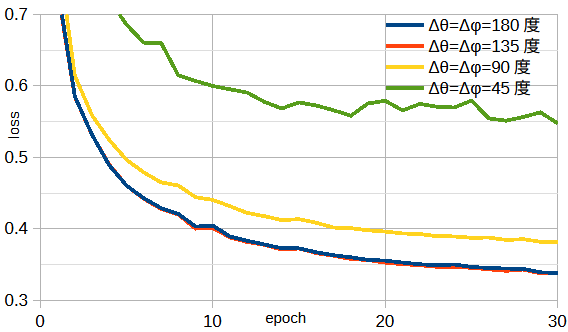
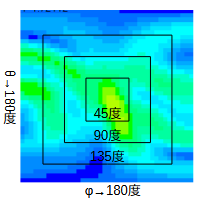
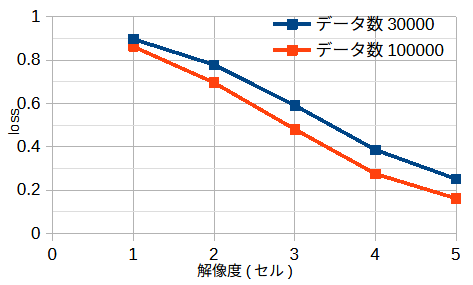
図3-6にデータ数と損失の関係を示します。
図から、データ数が増えると、損失が小さくなることがわかります。
なお、データ数300000はメモリー不足のために Amazon EC2 [8] を使用しています。
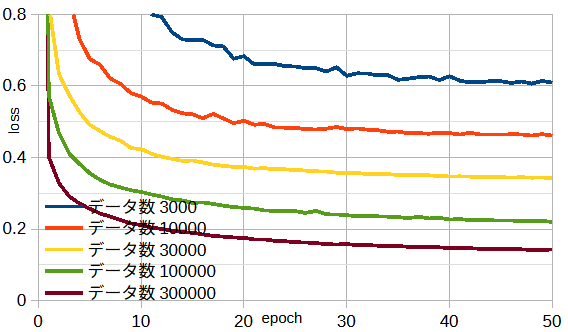
図3-7にデータ数と最小損失の関係(図3-6の最小値)を示します。
図から、データ数が増えると、損失が小さくなることがわかります(スケーリング則)。
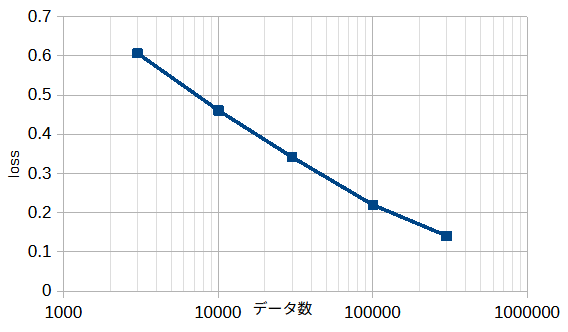
図3-8に電流分布の推定結果を示します。
図は2個1組になっており、左が正解値、右が推定値です。
左の黒数字はデータ番号と電流最大値、右の赤数字はデータ番号と電流値の誤差の平均です。
(a)は線分電流、(b)はセル電流です。
すべてのデータで推定と正解がよく合っていることがわかります。

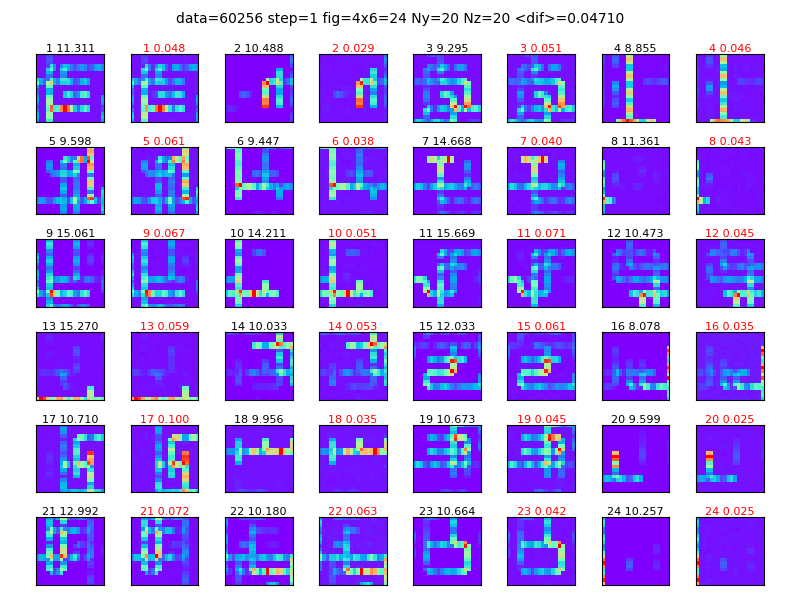
図3-8 電流分布の推定結果(データ数=300000, ResNet34重みなし)
ここまでの計算は解像度(最小座標単位)=4セルで行ってきましたが、
図3-9に解像度を変えたときの損失を示します。
解像度3のときのみその倍数にするためにNy=Nz=21としています。
解像度が小さくなるとより多様なアンテナ形状を対象にすることができますが、
形状の自由度が増えるのでより多くの学習データが必要になります。
以上で述べたように、放射パターンには位相が必要ですが、
放射パターンの測定値の位相は相対的なものです。
ここでは一つのアンテナ(ループアンテナ)をとり、
給電電圧に因子exp(jφi) (φi=2πi/Nφ, Nφ=24)
をかけて放射パターンを計算します。そのとき放射パターンにも同じ因子がかけられます。
上で学習したモデルでそれぞれの放射パターンを推論した結果を図3-10に示します。
2個1組で、左は正解、右は推定です(振幅は一定なので正解はすべて同じものです)。
図から、すべてのケースで電流分布はほぼ正しく推定されています。
以上から、給電電圧の位相は不明でも、
放射パターンの位相を正しく測定すれば電流分布は推定できることがわかります。
