特に断らない限り、モーメント法の計算条件は以下の通りです。
深層学習の計算条件は以下の通りです。

図4-2に電磁界成分が|Ex|,|Ey|,|Ez|,|Hx|,|Hy|,|Hz|の振幅のみの6成分のときの損失を示す。
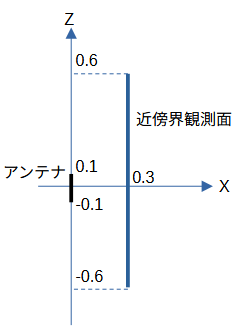
アンテナからの距離を4通り考えます。
アンテナ中心(原点)から見込む観測面の角度は一定です。
参考までに、フレネル領域の範囲は R < 2D2/λ = 2*0.22/0.1 = 0.8m です。
図から振幅のみのときは損失が大きく、
振幅のみからアンテナ上の電流分布を推定することは困難であることがわかります。
また、アンテナから離れるほど損失が大きくなります。
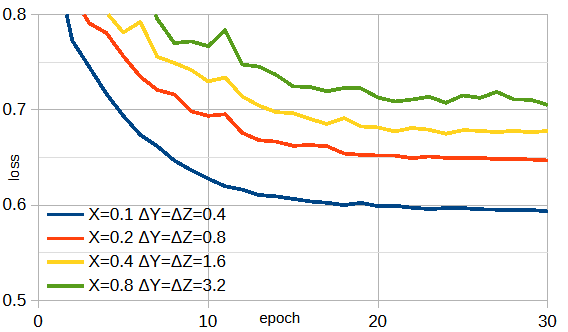
図4-3に6通りの電磁界複素数1成分の損失を示します。
図から、Exが最良でEyとEzがこれに続き、磁界の3成分は同等であることがわかります。
縦波成分であるExが最良であることが近傍界に特徴的な性質です(遠方界には縦波成分はない)。
EyとEzがExに劣る理由は一般にアンテナの偏波は直線偏波に近いので、
EyとEzの一方のみではアンテナの電流分布を十分に推定できないためと思われます。
磁界が電界に劣りかつ3成分が同じ性能である理由は不明です
(アンテナ形状に起因する可能性があります)。
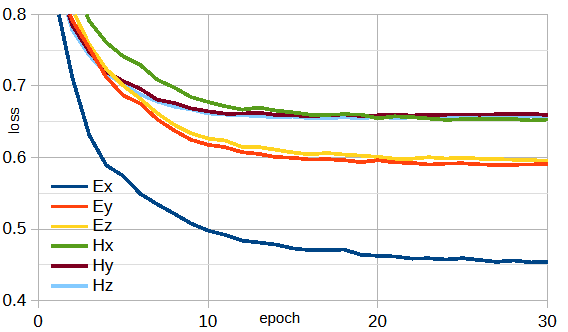
図4-4に2成分以上の電磁界複素数成分の損失を示します。
図から、成分数を増やしても図4-3のEx1成分とほぼ同じであることがわかります。
以下では、Ey,Ez成分(Re(Ey),Im(Ey),Re(Ez),Im(Ez))を考えます。
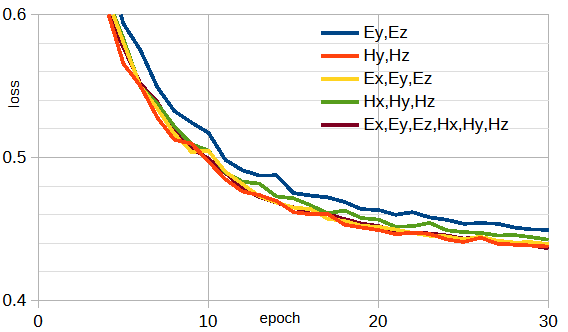
図4-5にResNet18/34/50の重みあり/なしの損失を示します。
不規則な傾向が見られますが、以下ではResNet18重みなしを使用します。
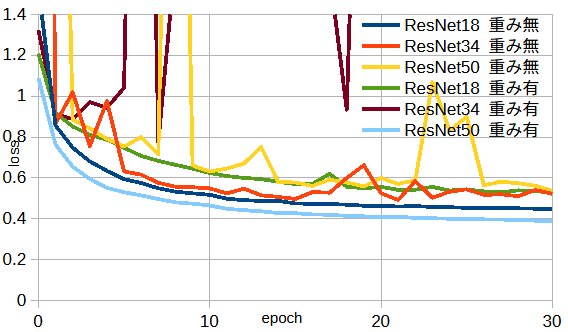
図4-6にデータ数と損失の関係を示します。
図から、データ数が増えると、損失が小さくなることがわかります。
なお、データ数300000はメモリー不足のために Amazon EC2 [8] を使用しています。
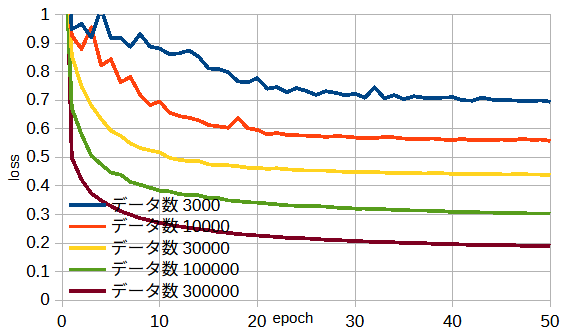
図4-7にデータ数と最小損失の関係(図4-6の最小値)を示します。
図から、データ数が増えると、損失が小さくなることがわかります(スケーリング則)。
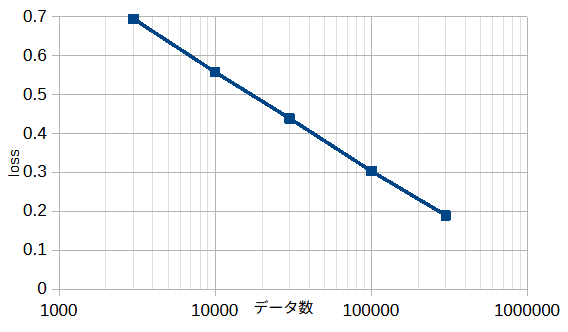
図4-8に電流分布の推定結果を示します。
図は2個1組になっており、左が正解値、右が推定値です。
左の黒数字はデータ番号と電流最大値、右の赤数字はデータ番号と電流値の誤差の平均です。
(a)は線分電流、(b)はセル電流です。
すべてのデータで推定と正解がよく合っていることがわかります。

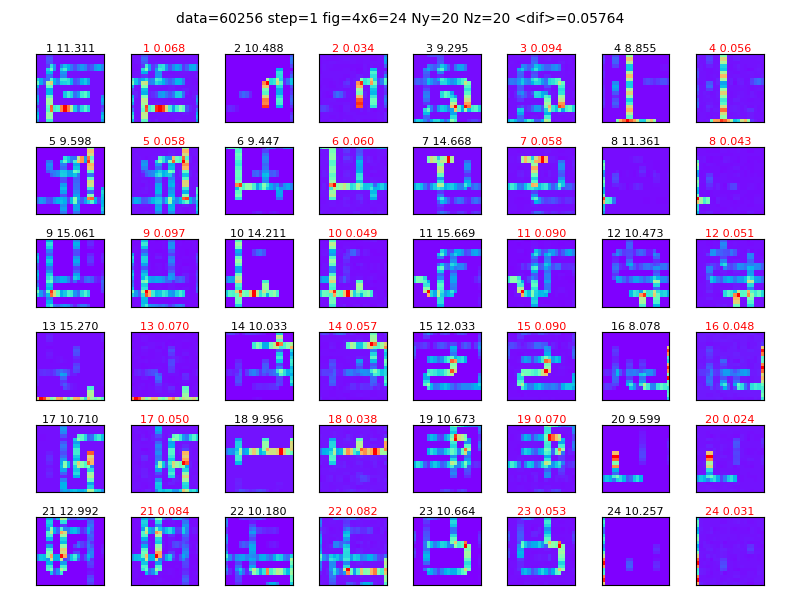
図4-8 電流分布の推定結果(データ数=300000, ResNet18重みなし)