目次

2. 計算手法

2.1 処理の流れ

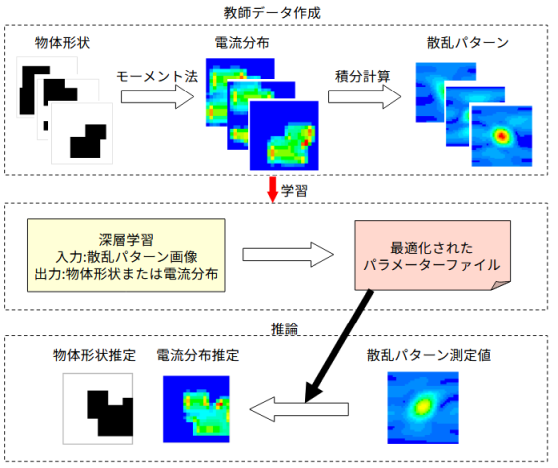
図2-1に処理の流れを示します。
以下の三つの部分から成ります。

  1. 教師データ作成: 多数の物体形状を作成し、モーメント法により電流分布と散乱パターンを計算します。
  2. 学習: 深層学習により教師データを学習し、最適化されたパラメーターファイルファイルを得ます。
  3. 推論: パラメーターファイルファイルを用いて散乱パターン測定値から物体形状または電流分布を推定します。


図2-1 処理の流れ

2.2 物体形状

物体形状は平面内の4個の完全導体の長方形の集合とします。
全体の領域を縦横20個のメッシュとします。メッシュの1単位をセルと呼びます。
各長方形の中心をランダムにとり、その縦と横の長さは2セルから8セルまでのランダムな値とします。
図2-2に40個の物体形状の例を示します。 平均的に約30%の領域が物体で占有されます。


図2-2 物体形状（20, 20, 4, 2, 8 モデル）

2.3 モーメント法

2.3.1 モーメント法の計算モデル

図2-3にモーメント法の計算モデルを示します。
物体はX面上にあるものとし、物体を導線の集合で表すワイヤグリッドモデルを採用します。
これに+X方向（θ=90度、φ=0度）から垂直偏波の平面波が入射するモデルを考えます。


図2-3 モーメント法の計算モデル（ワイヤグリッドモデル）

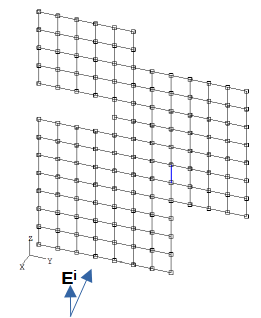
図2-4にモーメント法により電流分布を計算した結果を示します。 青→赤は電流の大きさを表します。


図2-4 電流分布

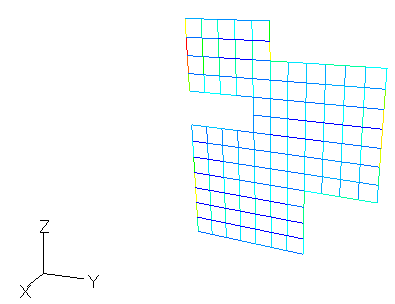
図2-5に全方向散乱パターンを示します。


図2-5 全方向散乱パターン

2.3.2 教師データ作成

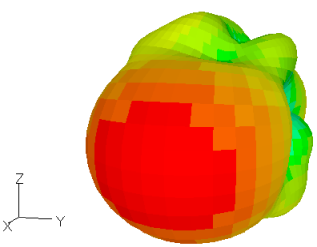
図2-6に40データの電流分布を示します。
ワイヤグリッド上の電流をセル中心の電流IxとIy（複素数）に補間したのち、 絶対値I=√(|Ix|2+|Iy|2)を表示しています。
垂直偏波であるために縦方向のエッジに大きい電流が流れます。
図の上の数値はデータ番号と電流最大値です。


図2-6 電流分布の教師データ

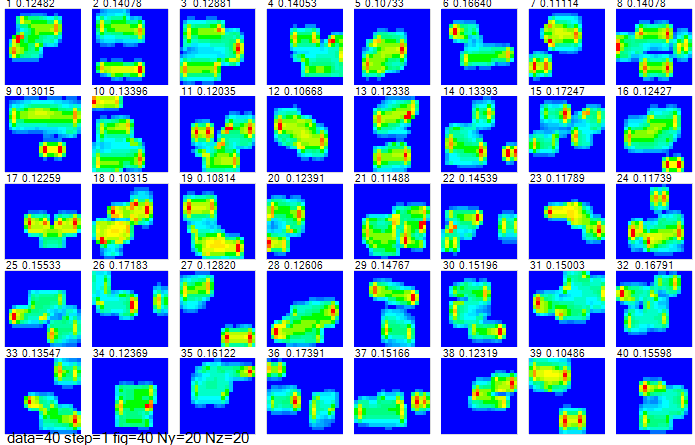
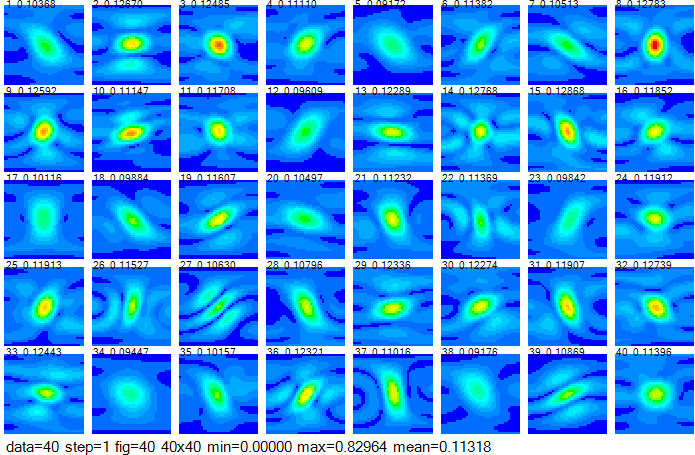
図2-7に40データの散乱パターンを示します。
縦軸は上から下へθ=0→180度、横軸は左から右へφ=-90→+90度です。
遠方界はEθとEφの2成分の複素数であり、 その絶対値E=√(|Eθ|2+|Eφ|2)を表示しています。
図から多くの場合、散乱パターンの中心は図の中心（すなわち入射方向）となっています。
平面波の入射方向を+Xとした理由は極座標で表したときに散乱パターンの中心を図の中心にするためです。
散乱パターンは物体形状の情報を含んでいます。
図の上の数値はデータ番号と平均値です。


図2-7 散乱パターンの教師データ（Δθ=180度、Δφ=180度）

2.4 深層学習

前項の方法で物体形状をランダムに変えて計算し、多数の教師データを作成します。
そのデータを用いて深層学習を行い、 散乱パターンから物体形状または電流分布を推定することを考えます。
深層学習には画像処理に適したCNN（畳み込みニューラルネットワーク）を用います。
以下では、散乱パターンを"image"、物体形状を"label1"、電流分布を"label2"と呼びます。

2.4.1 物体形状(label1)推定の損失

物体形状(label1)を推定するときの損失は式(2-1)とします。

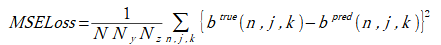　(2-1)
b(n,j,k)=0:セルに物体が存在しない、1:セルに物体が存在する　(2-2)

ここで、Nはデータ数、 btrueとbpredは物体形状の正解（教師データ）と推定値です。
btrueは0または1の2値ですが、 bpredは連続量であり、0～1の範囲を超えることもあります。
反復計算時の"損失(loss)"は式(2-1)の平方根とします。

2.4.2 電流分布(label2)推定の損失

電流分布(label2)を推定するときの損失は式(2-3)の2通りを考えます。
上の式は電流の絶対値のみを推定するとき、 下の式は電流の4成分を推定するときです。

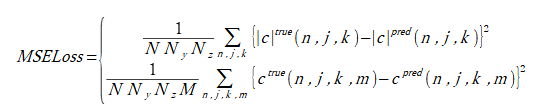　(2-3)
|c|=√(c(m=0)2 + c(m=1)2 + c(m=2)2 + c(m=3)2)　(2-4)
c(m=0) = Re(Iy), c(m=1) = Im(Iy), c(m=2) = Re(Iz), c(m=3) = Im(Iz)　(2-5)

ここで、Nはデータ数、M=4, ctrueとcpredは電流分布の正解（教師データ）と推定値です。
反復計算時の"損失(loss)"は式(2-3)の平方根とします。

2.4.3 学習部

リスト2-1に学習部のソースコードを示します。
ユーザーの行う作業は以下の2点です。

  1. 散乱パターンと物体形状または電流分布の教師データをdatasetに代入する
  2. モデル（ニューラルネットワーク）を定義する
その他は深層学習共通のコードです。

リスト2-1 学習部のソースコード(PyTorch)

dataset設定      ※1
dataloader設定
model設定        ※2
criterion = nn.MSELoss()                      # 損失関数: MSE
optimizer = optim.Adam(model.parameters())    # 最適化関数: Adam
for epoch in range(num_epochs):               # エポックに関するループ
    for data, target in train_loader:         # ミニバッチに関するループ
        optimizer.zero_grad()                 # 勾配初期化
        output = model(data)                  # 順伝搬
        loss = criterion(output, target)      # 損失計算
        loss.backward()                       # 逆伝搬
        optimizer.step()                      # 最適化関数更新

2.3.3 ResNet

ニューラルネットワークモデルにはResNet[6][7]を使用します。
ResNet18,ResNet34,ResNet50を考えます。
モデルを定義する方法は以下の通りです。
ゼロから（ランダムな初期値から）学習するには以下のいずれかになります。

model = models.resnet18(weights=None)
model = models.resnet34(weights=None)
model = models.resnet50(weights=None)
最適化されたパラメーターからファインチューニングするには以下のいずれかになります。
model = models.resnet18(weights=models.ResNet18_Weights.DEFAULT)
model = models.resnet34(weights=models.ResNet34_Weights.DEFAULT)
model = models.resnet50(weights=models.ResNet50_Weights.DEFAULT)
ここでは前者を「重みなし」、後者を「重みあり」と呼びます。
その後、以下のように入力サイズと出力サイズを変更します。
model.conv1 = nn.Conv2d(入力サイズ, 64, 7, stride=2, padding=3, bias=False)
model.fc = nn.Linear(model.fc.in_features, 出力サイズ)
入力サイズ = 散乱パターン成分数（通常4）
出力サイズ = Ny * Nz（物体形状推定時）, Ny * Nz * (1 or 4)（電流分布推定時）