特に断らない限り、モーメント法の計算条件は以下の通りです。
深層学習の計算条件は以下の通りです。
遠方界は複素数であるために、遠方界の成分数として、
|Eθ|,|Eφ|の2成分をとる方法と、
Re(Eθ),Im(Eθ),Re(Eφ),Im(Eφ)の4成分をとる方法があります。
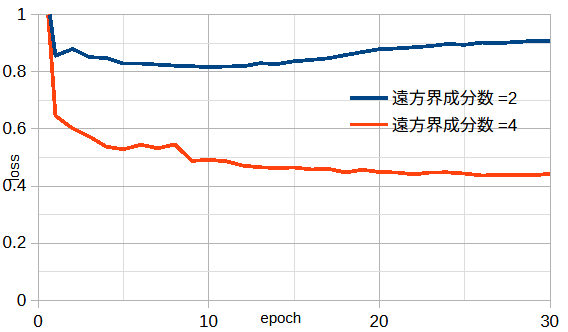
図3-1に両者の損失を比較します。これから遠方界成分数=2のときは損失が大きいことがわかります。

図3-2に物体形状の推定結果の1例を示します。
それぞれ3個の図からなり、
左から順に正解btrue、推定bpred、判定bpred01です。
ここで判定は式(3-1)で定義されます。
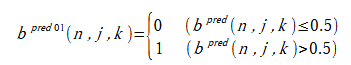 (3-1)
(3-1)
遠方界成分数=2のときは推定と判定ともに大きな誤差があることがわかります。
以上から、遠方界には振幅と位相の両方が必要であることがわかります。
以下では、遠方界成分数=4とします。
なお、位相の測定には距離のあいまいさがあるために、
何らかの基準物体で校正する必要があります。
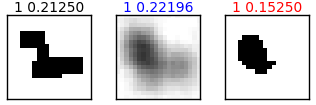

図3-2 遠方界成分数と物体形状推定の関係(label1, データ数=10000)
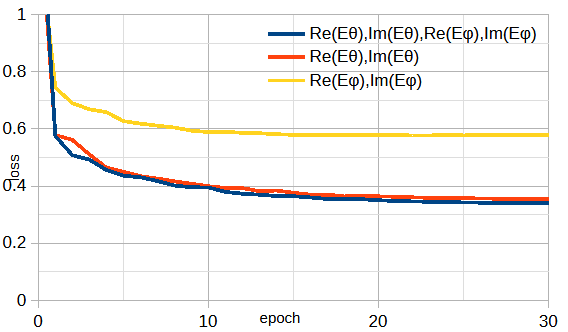
参考までに、図3-3に遠方界成分について主偏波(Eθ)のみと交差偏波(Eφ)のみの結果と比較した結果を示します。
本ケースは直線偏波であるために主偏波と交差偏波に大きな差が出ますが、
一般の偏波を考えるとEθとEφの両方を測定することが望ましいです。
電流分布の成分数は式(2-3)のように2通りあります。
上を電流成分数=1、下を電流成分数=4と呼びます。
図3-4に損失を示します。両者は同じふるまいを示します。
損失の計算式が異なるために単純に優劣を比較することはできません。
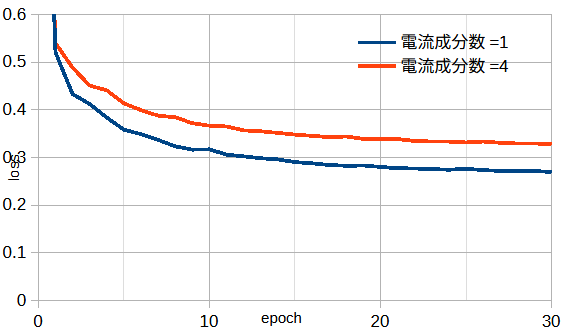
図3-5に電流分布の推定結果を3例示します。
左は正解ctrue、右は推定結果cpredです。
電流成分数=1と電流成分数=4の性能は同程度と思われます。
以下では、電流成分数=1とします。
なお、物体の存在しない所には電流は流れないために、
電流分布の推定は物体形状の推定を兼ねています。
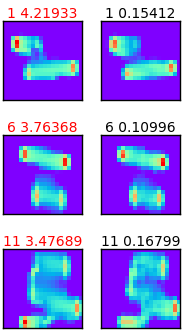
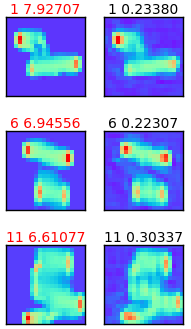
図3-5 電流成分数と電流分布推定の関係(label2, データ数=30000)
図3-6にResNet18/34/50の重みあり/なしの損失を示します。
ResNet18/34の重みなしとResNet50の重みありの性能が優れているという不規則な結果になっています。
ResNet18/34/50のepochあたりの計算時間は7/12/15秒です。
以下では、性能と計算時間を考慮してResNet18重みなしを使用します。
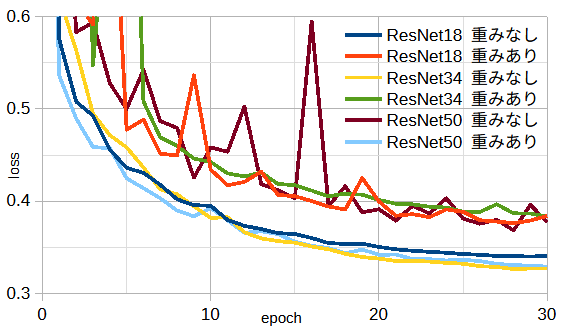
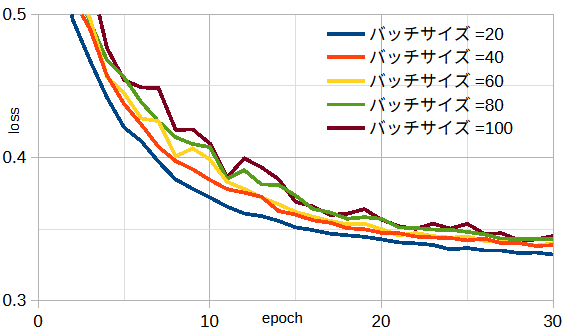
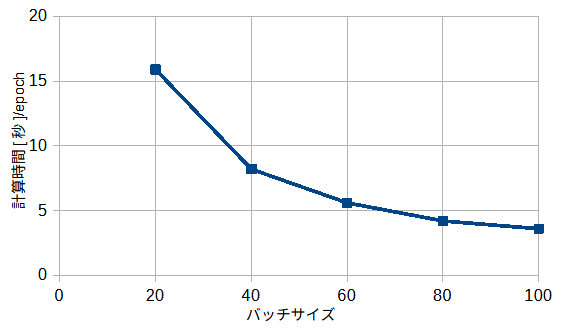
図3-7と図3-8にバッチサイズを変えた時の損失と計算時間を示します。
これから、バッチサイズを大きくすると損失は少し大きくなり、計算時間は小さくなります。
なお、使用メモリーはバッチサイズに無関係です。
以下では、性能と計算時間を考慮してバッチサイズ=60とします。
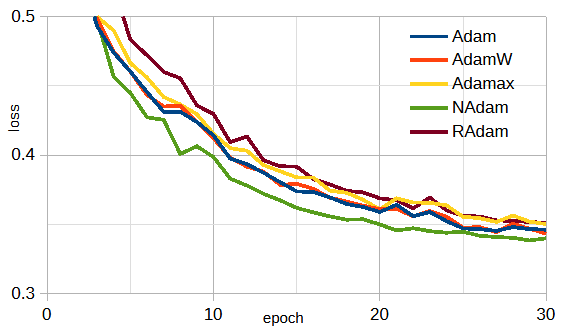
PyTorchには5種類のAdam系最適化関数が用意されています。
図3-9にそれらを比較した結果を示します。
大きな違いはありませんが、強いて言えばNAdamが優れています。
以下では、NAdamを使用します。
学習の前処理として、imageとlabelに下記の操作を行って標準正規分布にすることを正規化と呼びます。
image = (image - image.mean()) / image.std() label = (label - label.mean()) / label.std()図3-10にimageとlabelの正規化の有無を比較します。
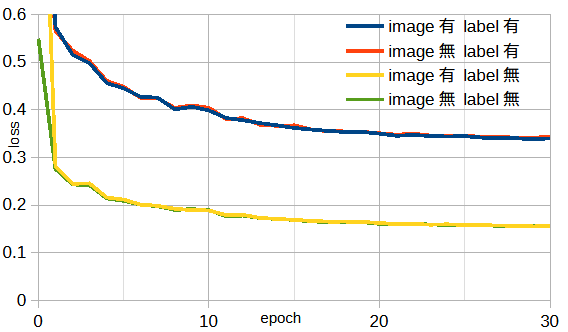
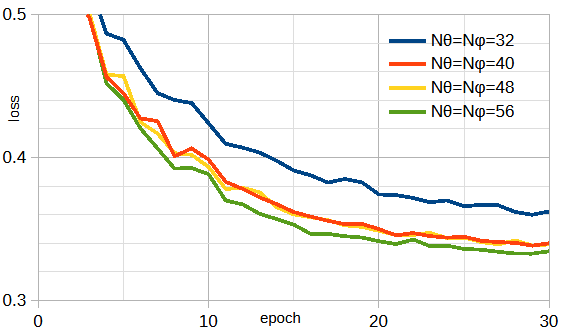
図3-11に遠方界パターンの角度分割数(Nθ,Nφ)を変えたときの損失を示します。
Nθ=Nφ=40,48の結果は同じですが、
一般的にNθ,Nφが大きくなると損失が小さくなることがわかります。
物体形状(label1)の推定のときは次式でaccuracy(正解率)を定義することができます。
accuracy1は推定の正解率、accuracy2は判定の正解率です。
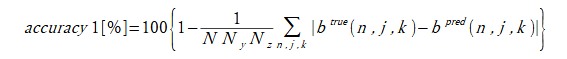 (3-2)
(3-2)
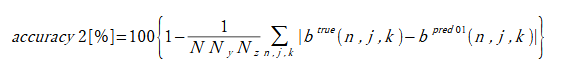 (3-3)
(3-3)
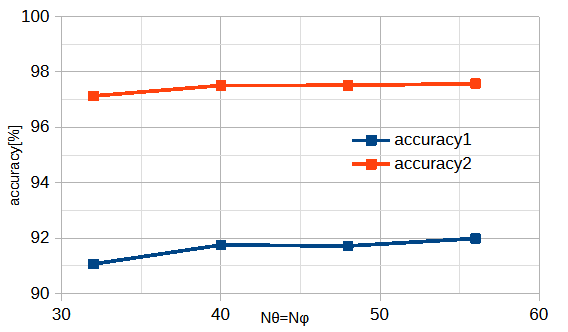
図3-12に遠方界分割数を変えたときのそれぞれの正解率を示します。
学習時の使用メモリーはimageの画素数(=Nθ×Nφ)にほぼ比例します。
以上から、計算精度、計算時間、使用メモリーを考慮して
Nθ=Nφ=40 とします。
ここまでの計算では、遠方界の角度範囲を半球全体すなわちΔθ=180度(θ=0~180度)、
Δφ=180度(φ=-90~+90度)としましたが、
角度範囲を狭くしたときの損失を図3-13に示します。
図から、角度範囲Δθ=Δφ=120度までは大きな違いはなく、
これより狭くなると急激に損失が大きくなることがわかります。
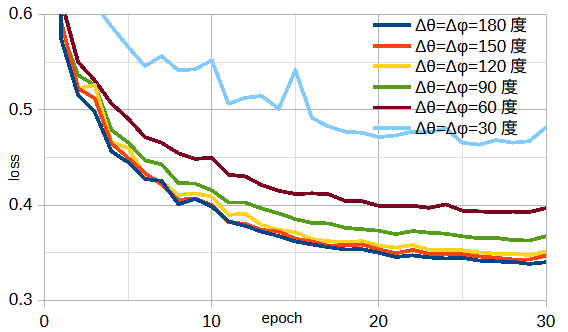
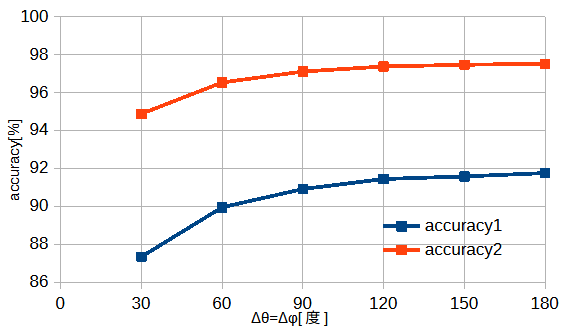
図3-14に角度範囲Δθ=Δφを変えたときの正解率を示します。
図3-13と同じ傾向が見られます。
以上から、遠方界の角度範囲を半球全体より狭くしても、
物体形状を推定できることがわかります。
なお、物体が大きくなるか、周波数が高くなると、
散乱パターンのビーム幅が小さくなりローブ数が増えるために、
より少ない角度範囲で物体形状を推定することが可能になります。