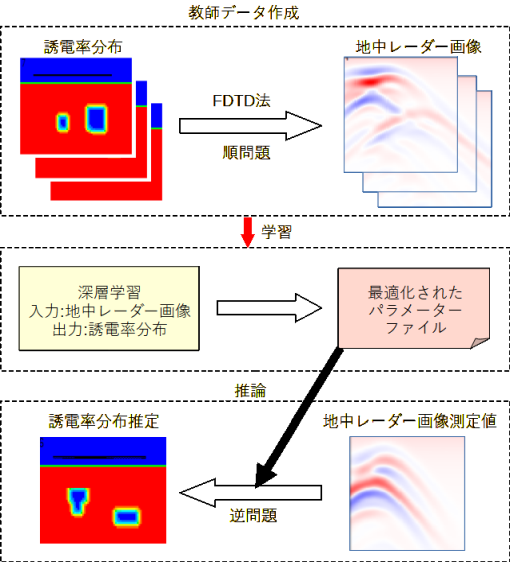
図2-1に処理の流れを示します。
以下の三つの部分から成ります。

図2-2に2次元のFDTD法の計算モデルを示します。
地下に誘電体を含む領域をとり、地上に送信アンテナと受信アンテナを置きます。
FDTD法の計算領域は地下と地上から成ります。計算領域の外部にPML層を置きます。
送信アンテナからパルスを放射し、近くにある受信アンテナの電界の時間波形を計算します。
送信アンテナと受信アンテナを水平方向に平行移動させて同様の計算を繰り返し行います。
3次元モデルも同様に考え、垂直方向をZ方向、水平方向をXY方向とします。
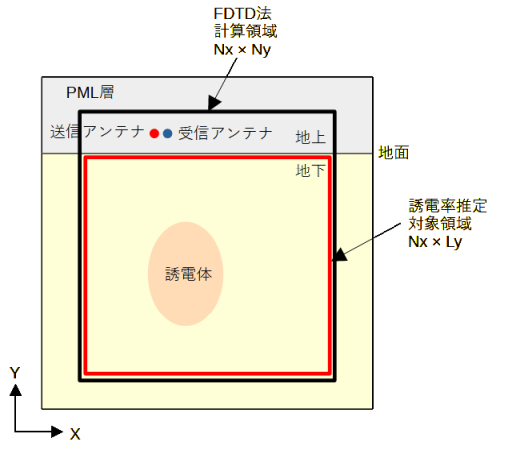
図2-3に送信アンテナの時間波形を示します。
ガウスパルスと微分ガウスパルスの2通りを考えます。
微分ガウスパルスは直流成分を持たない特長があります。
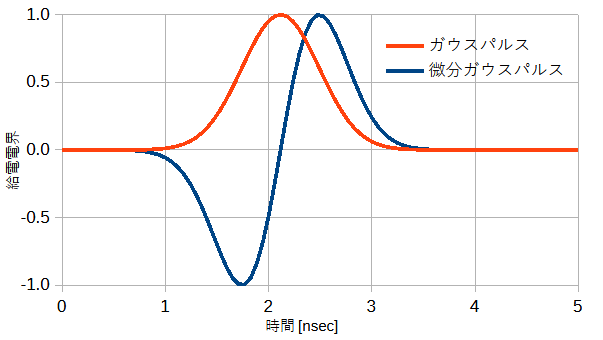
図2-4に地下の誘電体分布を適当にとったときの受信アンテナの受信波形を示します。
(b)は縦軸を拡大した図です。
最初に送信アンテナからの大きな直接波が観測されますが、
これは地下の情報を含まないために利用しません。
微分ガウスパルスは送信波形に二つのピークを持つために受信波形の変動も大きい傾向があります。
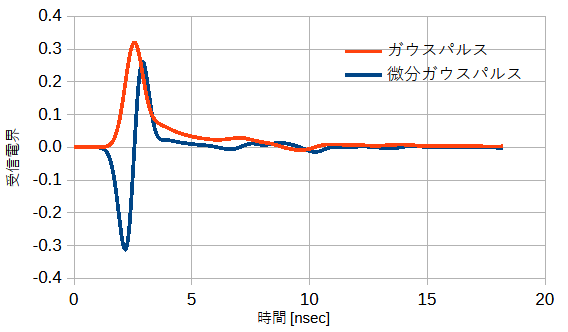
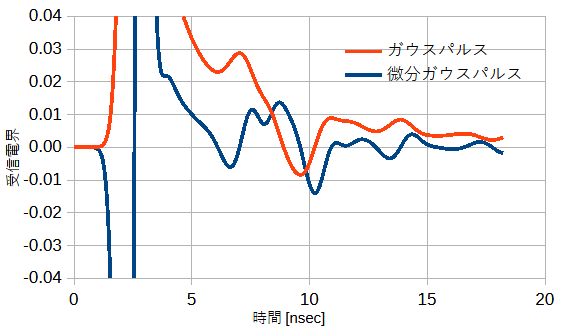
図2-4 受信波形
図2-5に電界分布の一例を示します。
各点における時間波形を指定した周波数でフーリエ変換したものです。
電界分布は地中レーダーでは直接使用しませんが、計算結果の確認に使用することができます。
図から計算領域の境界で不自然な反射波は見られず、
吸収境界条件(PML)が正しく機能していることもわかります。
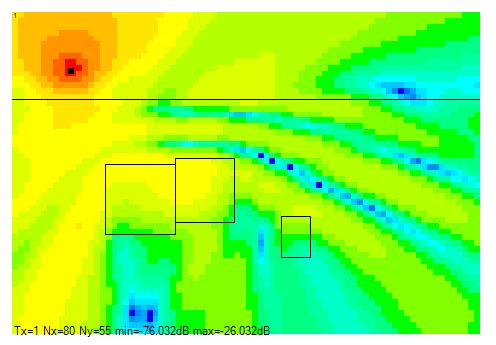
図2-6に順問題と逆問題の関係を示します。
上で述べた方法により誘電率分布から地中レーダー画像を求めることが順問題です。
逆に地中レーダー画像から誘電率分布を求めることが逆問題であり、本プログラムの目的です。
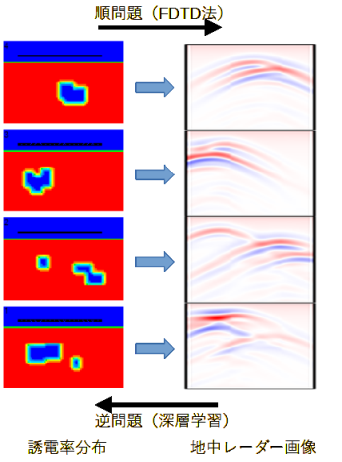
前項の方法で誘電体分布をランダムに変えて計算し、
多数の誘電体分布と地中レーダー画像の組(教師データ)を求めます。
そのデータを用いて深層学習を行い、地中レーダー画像から誘電率分布を推定することを考えます。
深層学習にはCNN(畳み込みニューラルネットワーク)を用います。
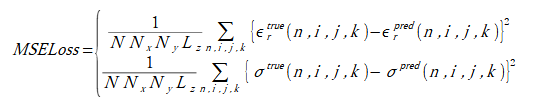 (2-1)
(2-1)
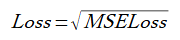 (2-2)
(2-2)
リスト2-1に学習部のソースコードを示します。
ユーザーの行う作業は以下の2点です。
リスト2-1 学習部のソースコード(PyTorch)
dataset設定 ※1
dataloader設定
model設定 ※2
criterion = nn.MSELoss() # 損失関数: MSE
optimizer = optim.Adam(model.parameters()) # 最適化関数: Adam
for epoch in range(num_epochs): # エポックに関するループ
for data, target in train_loader: # ミニバッチに関するループ
optimizer.zero_grad() # 勾配初期化
output = model(data) # 順伝搬
loss = criterion(output, target) # 損失計算
loss.backward() # 逆伝搬
optimizer.step() # 最適化関数更新
ニューラルネットワークモデルにはResNet[7][8]を使用します。
ResNet18,ResNet34,ResNet50を考えます。
モデルを定義する方法は以下の通りです。
ゼロから(ランダムな初期値から)学習するには以下のいずれかになります。
model = models.resnet18(weights=None) model = models.resnet34(weights=None) model = models.resnet50(weights=None)最適化されたパラメーターからファインチューニングするには以下のいずれかになります。
model = models.resnet18(weights=models.ResNet18_Weights.DEFAULT) model = models.resnet34(weights=models.ResNet34_Weights.DEFAULT) model = models.resnet50(weights=models.ResNet50_Weights.DEFAULT)ここでは前者を「重みなし」、後者を「重みあり」と呼びます。
model.conv1 = nn.Conv2d(入力サイズ, 64, kernel_size=7, stride=2, padding=3, bias=False) model.fc = nn.Linear(model.fc.in_features, 出力サイズ)入力サイズ = 受信アンテナ数 = 1(2D), 1以上(3D)