
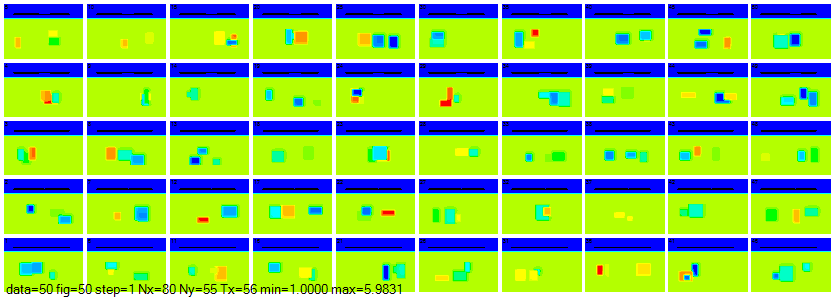

図3-1 誘電率分布
2次元モデルのFDTD法の計算条件は以下の通りです。
深層学習の計算条件は以下の通りです。
地下に3個の長方形を置きます。それぞれの位置と縦横の長さをランダムにとります。
誘電率分布としては以下の3ケースを考えます。
(1) ケース1
(2) ケース2
(3) ケース3
誘電率分布の不連続を緩和するために次式の5点平均化を1回行っています(導電率も同様)。
FDTD法では電気定数が不連続なYee格子点では両側の電気定数の平均値をとると計算精度が上がることが知られています。([1]p.39)
εr(i,j) ← {εr(i,j)+εr(i-1,j)+εr(i+1,j)+εr(i,j-1)+εr(i,j+1)}/5
図3-1に教師データの誘電率分布の一部を示します。
青→赤で誘電率が高くなることを表しています。
図(a)では地中と長方形の誘電率は一定です。
図(b)では地中の誘電率は一定、長方形の誘電率はランダムです。
図(c)では一定の割合で地下が2層に分割されていることと、
誘電率がランダムに設定されていることがわかります。
教師データから一定の割合(例えば80%)をランダムに選んで訓練データとし、
残りは検証のためのテストデータとします。



図3-1 誘電率分布
図3-2に6個の地中レーダー画像例を示します。
横軸は送信アンテナ位置、縦軸は受信波形の時間であり時間は上から下に進みます。
横方向のピクセル数は送信アンテナの数と同じ56であり、
縦方向のピクセル数はResNetを考慮して224としています。
送信アンテナからの直接波と地面からの反射波が経過した時間以降を取り出しています。
地中レーダー画像には地中の物体(誘電率の不連続)からの反射波による特徴的な双曲線が見られます。
その他、地中での電磁波の反射や散乱に起因する模様が見られます。
これらは地中の構造を反映しています。
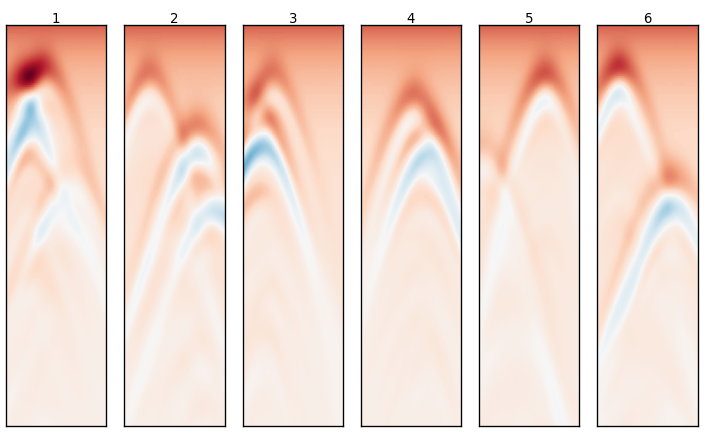
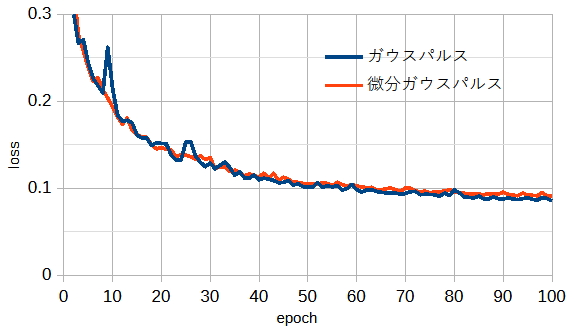
図3-3にパルス波形を変えたときの損失の収束状況を示します。
これから損失はパルス波形によってあまり変わらないことがわかります。
以下ではガウスパルスを考えます。
(ケース2, データ数=30000, ResNet18, 重みあり, 56x224px, Adam)
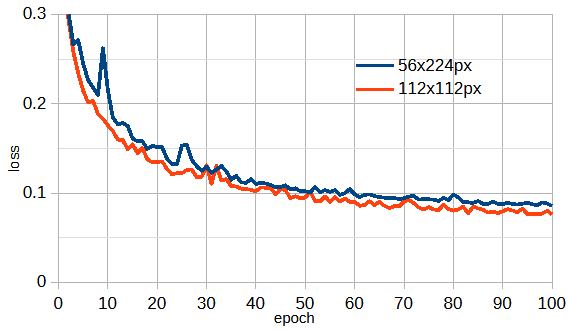
ResNetは画像サイズ224x224ピクセルのImageNet[9]向けに学習しているので、
画像サイズと縦横比がこれに近いほど精度がよいことが知られています。
図3-4に元の画像(56x224px)と変形した画像(112x112px)の損失の収束状況を示します。
両者の総ピクセル数は同じなので計算時間はほぼ同じです。
これから正方形画像(112x112px)のほうが損失が小さいことがわかります。
以下ではレーダー画像を112x112pxに変形したのちに学習を行います。
(PyTorchのtransforms.Resize関数を使用します)
(ケース2, データ数=30000, ResNet18, 重みあり, ガウスパルス, Adam)
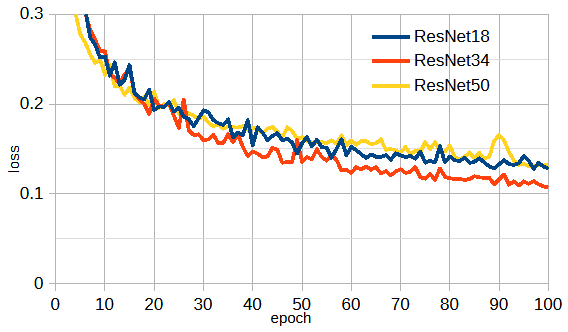
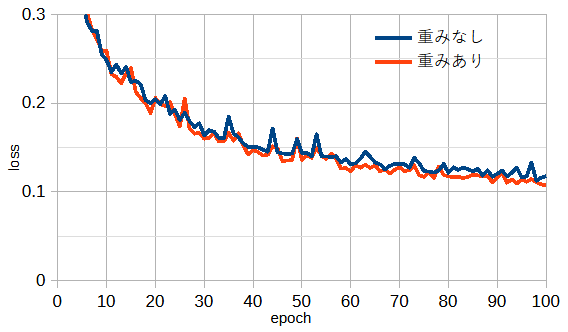
図3-5にResNet18/34/50の「重みなし」と「重みあり」の収束状況を示します。
ResNetの後の数字はネットワークの層数(畳み込みと全結合の和)を表します。
図から重みの有無の違いは小さいことがわかります。
これは本問題は深層学習の問題としては比較的容易であることを表しています。
ResNet18/34/50の1エポック当たりの計算時間は順に10/19/33秒です。
以下では計算精度と計算時間を考慮してResNet34重みありを使用します。
(ケース2, データ数=30000, ガウスパルス, 112x112px, Adam)
図3-6にミニバッチサイズ=25/50/100の収束状況を示します。
ミニバッチサイズ=25/50のとき損失が小さくなります。
ミニバッチサイズ=25/50/100の計算時間は順に3016/1874/1488秒です。
以上から、計算精度と計算時間を考慮してミニバッチサイズ=50とします。
(ケース2, データ数=30000, ガウスパルス, ResNet34重みあり, 112x112px, NAdam)
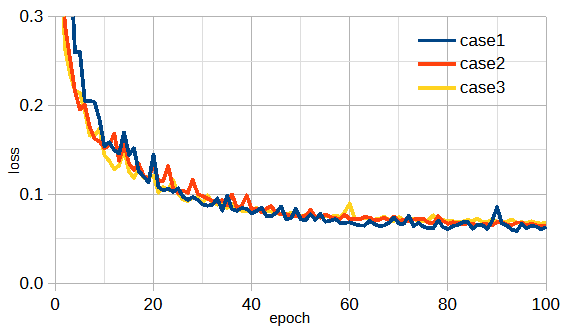
図3-7にケース1~3の損失の収束状況を示します。
これから誘電率分布が変わっても収束状況はほぼ同じであることがわかります。
(データ数=30000, ガウスパルス, ResNet34, 112x112px, NAdam)
図3-8にケース1~3のそれぞれ20個のデータの誘電率分布の推定結果を示します。
左が正解、右が推定値の2個1組のペアになっています。
すべてのデータについて場所、形、誘電率が正しく推定できていることがわかります。



図3-8 誘電率分布の推定結果(左:正解, 右:推論, データ数=30000, ガウスパルス, ResNet34, 112x112px, NAdam)
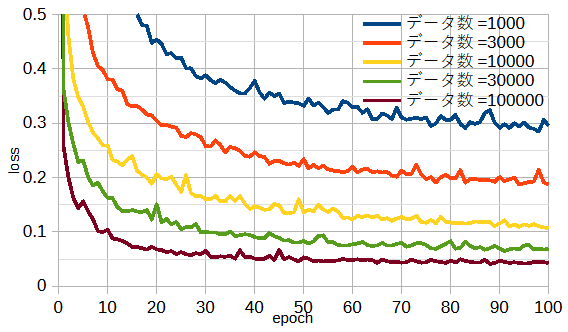
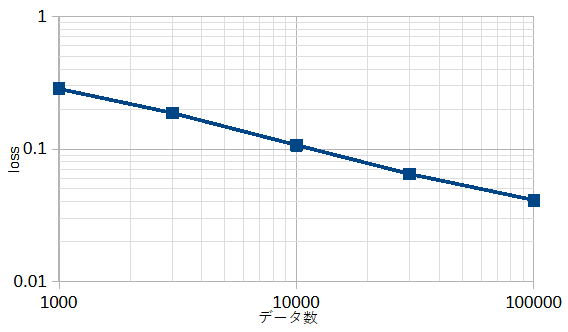
図3-9にデータ数を変えたときの収束状況を示します。
データ数が多いほど最終的な損失が小さいだけでなく収束も安定してかつ速いことがわかります。
(ケース2, ガウスパルス, ResNet34重みあり, 112x112px, NAdam)
図3-10にデータ数を変えたときの損失の最小値(図3-9の最小値)を示します。
データ数が多いほど損失が小さくなることがわかります。
データ数100000でも飽和しておらず、データ数をさらに増やすと性能が上がることが予想できます。
(スケール則)
(ケース2, ガウスパルス, ResNet34重みあり, 112x112px, NAdam)
PyTorchには最適化関数として5個のAdam系の関数が用意されています[10]。
最適化関数を変えるにはソースコードdlgpr.pyを以下のように変更します。
他の引数を指定せず既定値のハイパーパラメーターを使用しています。
optimizer = optim.Adam(model.parameters())図3-11に最適化関数を変えた時の損失の収束状況を示します。
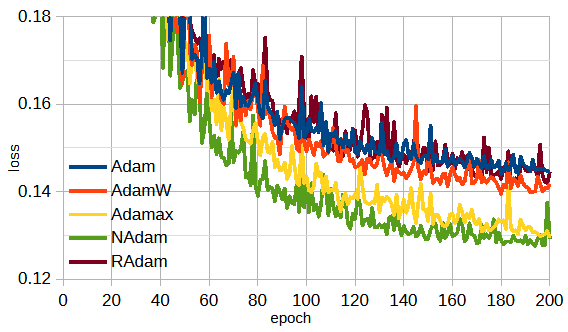
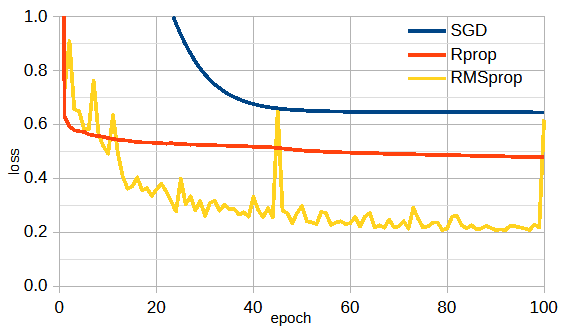
図3-11 最適化関数の比較
(ケース2, データ数=30000, ガウスパルス, ResNet34重みあり, 112x112px)
図3-12に導電率分布の推定結果を示します。
地中の電気定数はεr=4,σ=0、
長方形の電気定数はεr=4, σ=0.1S/mです。
導電率のみが異なるために損失は導電率について計算しています。
図(b)から導電率が正しく推定できることがわかります。
地中レーダー画像は地中の誘電率と導電率の両方を反映しているために、
両方を推定すると地中の構造に関してより多くの情報が得られます。
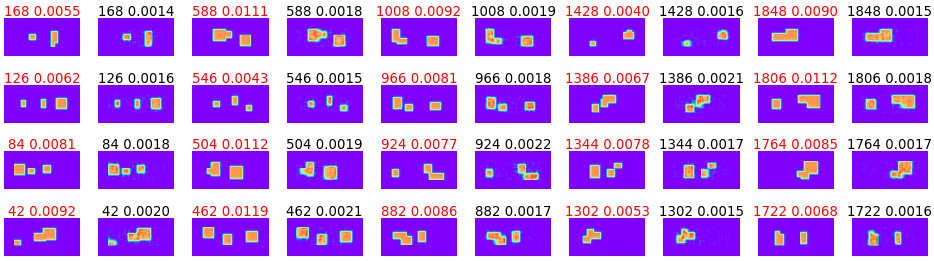
図3-12 導電率分布の推定(データ数=10000, ガウスパルス, ResNet34, 112x112px, NAdam)
導体は誘電体と比べて導電率が非常に大きくなります。
本プログラムではFDTD法の差分スキームに[1]の式(1.20c)を採用しているために、
導電率を大きくすると導体を表現することができます。
誘電体が導体とみなせる条件は以下のようになります。
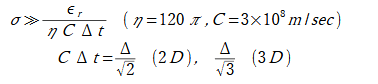 (3-1)
(3-1)
上式にεr=1,Δ=0.025mを代入すると、導体とみなせる条件は、
σ>>0.150S/m(2D),0.184S/m(3D)となります。
図3-13(a)にσ=3S/mのときの電界分布の3例を示します。
導体内では完全導体と同じく電界が0となることがわかります。
図(b)に導電率の推定結果を示します。導体の位置と形が正しく推定できていることがわかります。
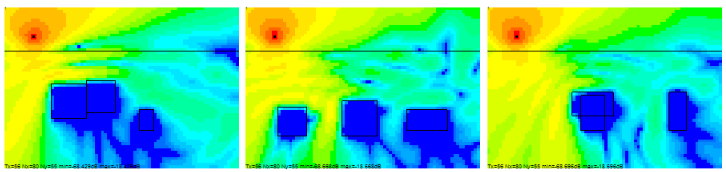

図3-13 導体の推定
図3-14に誘電体と導体が混在するときの導電率分布の推定結果を示します。
地中の電気定数はεr=4,σ=0一定、
長方形の比誘電率はεr=1一定とし, 導電率はσ=0~1S/mの範囲からランダムにとります。
図(b)において赤は導電率の大きい導体、青は導電率の小さい誘電体です。
どちらも正しく推定できることがわかります。
一般に中間の導電率の材質はないので学習の効率は悪いですが、
この方法でも導体と誘電体の両方を推定できることがわかります。
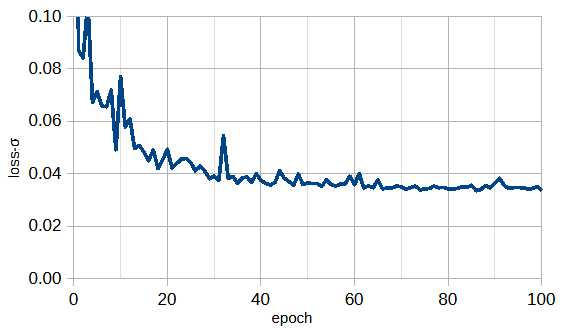

図3-14 誘電体と導体の混在するときの導電率分布の推定(データ数=30000, ガウスパルス, ResNet34, 112x112px, NAdam)
FDTD法を用いて教師データを作るときは、
送信パルス波形は地中レーダーの画像を取得するときの送信パルス波形に合わせたほうが望ましいが、
ここでは学習時のパルス波形と測定時のパルス波形が異なるときの影響を調べます。
表3-1に、誘電率分布としてケース1とケース2の2通り、
送信パルス波形としてガウスパルスと微分ガウスパルスの2通り、
合計4通りの組み合わせの損失を示します。
学習時と測定時の条件が一致する対角線上では損失が小さいですが、
それ以外のすべての組み合わせでは損失が大きいことがわかります。
| ↓学習 測定→ | ケース1 ガウスパルス | ケース1 微分ガウスパルス | ケース2 ガウスパルス | ケース2 微分ガウスパルス |
|---|---|---|---|---|
| ケース1 ガウスパルス | 0.137 | 0.607 | 0.644 | 0.673 |
| ケース1 微分ガウスパルス | 0.713 | 0.134 | 0.743 | 0.600 |
| ケース2 ガウスパルス | 0.487 | 0.673 | 0.132 | 0.480 |
| ケース2 微分ガウスパルス | 0.654 | 0.529 | 0.563 | 0.119 |
上記の問題を解決するために、
ガウスパルスと微分ガウスパルスを半々にとった教師データから学習することを考えます。
表3-2に混合パルス波形で学習した結果を示します。
同一パルスで学習した結果から劣化しますが、
異なるパルスの結果もある程度正しく推論できることがわかります。
誘電率分布が学習時と測定時が異なるときの推論結果は表3-1と同程度に悪いことがわかります。
| ↓学習 測定→ | ケース1 ガウスパルス | ケース1 微分ガウスパルス | ケース2 ガウスパルス | ケース2 微分ガウスパルス |
|---|---|---|---|---|
| ケース1 | 0.237 | 0.292 | 0.652 | 0.635 |
| ケース2 | 0.514 | 0.438 | 0.323 | 0.231 |
図3-15に誘電率分布が学習時と測定時が同じときの、
混合パルス波形の学習結果を示します(表3-2で色をつけた組み合わせ)。

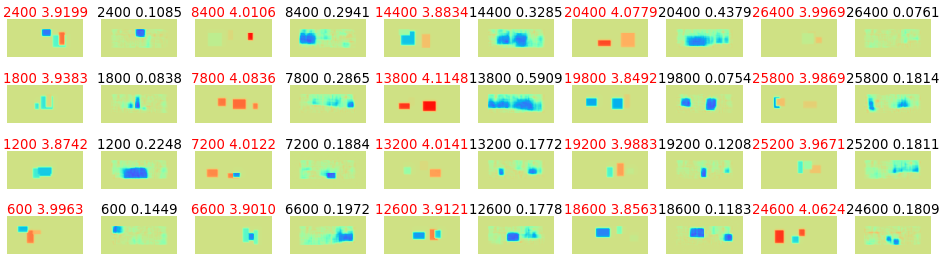


図3-15 混合パルス波形の学習の効果
(左:正解, 右:推論, データ数=10000, ResNet34, 112x112px, Adam)
学習データに使用する誘電率分布は、運用時の誘電率分布に近いことが大切です。
ケース1は地中と埋設物の誘電率が固定であり、
ケース2は地中の誘電率は固定であり埋設物の誘電率はランダムに変わります。
ケース2は特殊なケースとしてケース1を含んでいます。
学習時と推論時の誘電率が同じであればすでに述べたように正しく推論されます。
図3-16に学習時と推論時の誘電率が異なるときの推定結果を示します。
図(a)では比較的正しく推定され、図(b)では推定結果には大きな誤差があります。

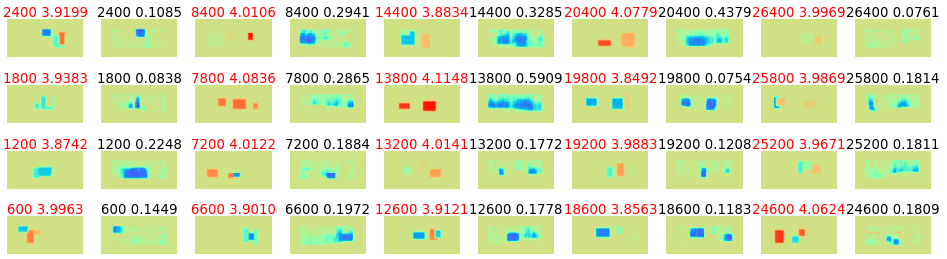
図3-16 学習データと異なる誘電率分布の推論
(左:正解, 右:推論, ガウスパルス, データ数=30000, ResNet34, 112x112px, NAdam)
背景(地中の埋設物がない所)の誘電率は一般には正確にわかりませんが、
適当な値を設定して学習することが必要です。
図3-17は背景の比誘電率εr=4で学習したモデルで、
背景の比誘電率εr=3のときのレーダー画像を推論した結果です。
ただし埋設物の比誘電率εr=1、背景と埋設物の導電率σ=0としています。
図から、背景の比誘電率εr=4と間違えていますが、
埋設物の形と比誘電率はほぼ正しく推定できています。

(左:正解, 右:推論、データ数=100000, ガウスパルス, ResNet34重みあり, 112x112px, NAdam)
学習データは3.2の通り3個のランダムな長方形の集合ですが、
図3-18にこれと異なる形状である三角形と円の地中レーダー画像の推定結果を示します。
三角形と円もある程度正しく推定できることがわかります。
学習データの中には三角形と円にある程度近い形状も存在すると考えられます。
学習データと異なる形状の推定精度をより上げるには、
学習データ数を増やすか、学習データの長方形の数を増やすことが有効と思われます。
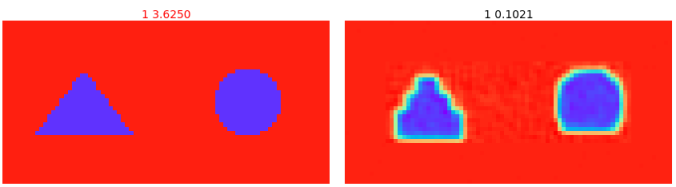
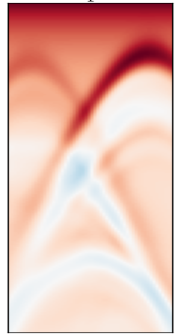
(左:誘電率分布正解, 中:誘電率分布推定, 右:地中レーダー画像)
(ケース1, データ数=30000, ガウスパルス, ResNet34重みあり, 112x112px, NAdam)
図3-19に6通りの乱数の収束状況を示します。
乱数1~4は関数urandの引数です。
乱数5/6はNumPy/PyTorchの乱数をファイルに出力して読み込んだものです。
図から乱数によって結果は変わらないことがわかります。
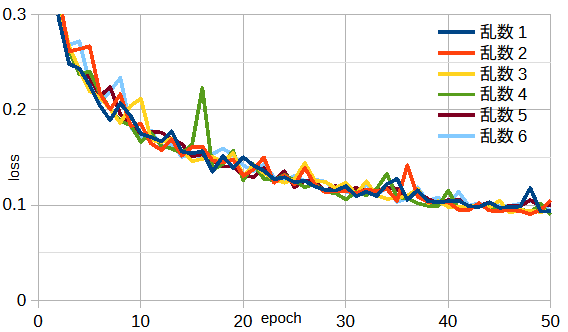
(ケース1, データ数=30000, ガウスパルス, ResNet18重みあり, 112x112px, Adam)