3次元モデルのFDTD法の計算条件は以下の通りです。
深層学習の計算条件は以下の通りです。
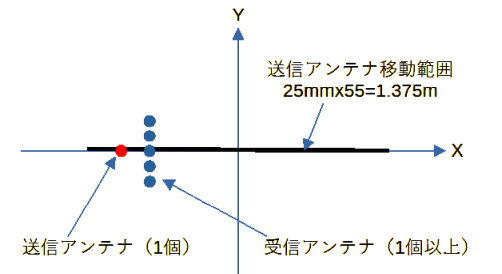
図4-1に送受信アンテナの位置を示します。
X軸に沿って1個の送信アンテナを移動し、その近くに1個以上の受信アンテナを置きます。
送信アンテナと受信アンテナは連動して移動します。

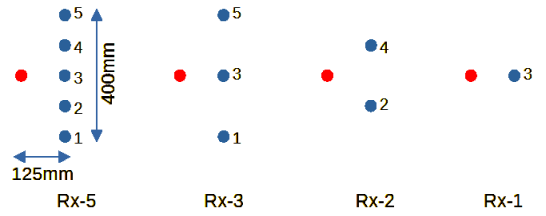
受信アンテナの数と位置としては、図4-2の4通りを考えます。
それぞれ、Rx-5, Rx-3, Rx-2, Rx-1 と呼びます。
誘電率分布として2次元モデルのケース1を考えます。
すなわち、均質な地下媒質中(εr=4)にランダムな形の直方体をランダムな位置に置きます。
直方体の材質は空気(空洞)、直方体の数は2個とします。
誘電率を滑らかに変化させるために以下の7点平均化を1回行っています。
εr(i,j,k) ← {εr(i,j,k)+εr(i-1,j,k)+εr(i+1,j,k)+εr(i,j-1,k)+εr(i,j+1,k)+εr(i,j,k-1)+εr(i,j,k+1)}/7
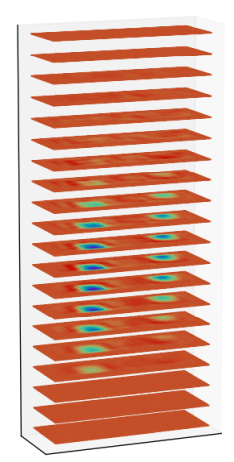
図4-3に1つのデータの誘電率分布を示します。
Z面でスライスした図を順に示しています。全部でLz=40枚あります。
場所と大きさが異なる2個の直方体が存在することがわかります。

図4-4に受信アンテナの数と位置を変えた時の損失の収束状況を示します。
これからRx-1以外はほぼ同じ性能であることがわかります。
Rx-1は左右の位置が判別できないので3次元モデルには適していないことは予想通りです。
以上から、適度に離れた受信アンテナが最低2個あれば十分であることがわかります。
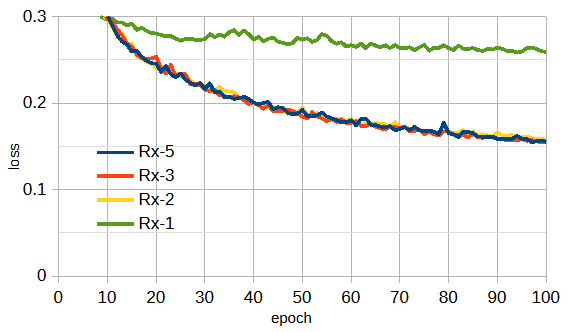
(データ数=10000, ResNet34重みあり, ガウスパルス, 112x112px)
図4-5に ResNet18, ResNet34, ResNet50 の損失の収束状況を示します。
エポック当たりの計算時間は順に10/13/29秒です。
図から差は小さいですがResNet34とResNet50が性能がよいことがわかります。
以下ではResNet34を使用します。
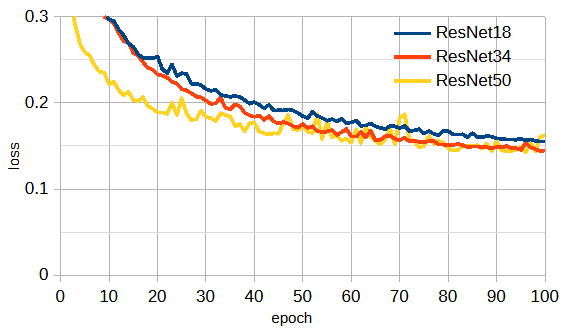
(データ数=10000, Rx-3, ガウスパルス, 112x112px)
図4-6にデータ数を変えたときの収束状況を示します。
2次元モデルと同じく、
データ数が多いほど最終的な損失が小さいだけでなく収束も安定してかつ速いことがわかります。
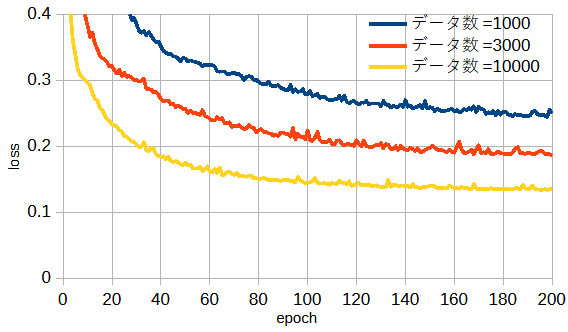
(ResNet34, Rx-3, ガウスパルス, 112x112px)
図4-7にデータ数を変えたときの損失の最小値(図4-6の最小値)を示します。
2次元モデルと同じく、
データ数が多いほど損失が小さくなることがわかります。
データ数10000でも飽和しておらず、データ数をさらに増やすと性能が上がることが予想できます。
(スケール則)
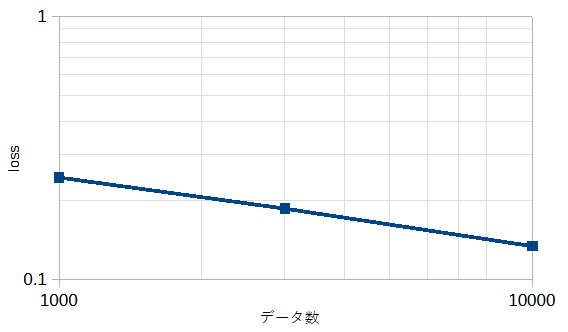
(ResNet34, Rx-3, ガウスパルス, 112x112px)
図4-8に3個のデータの誘電率分布の推定結果を示します。
Z面についてスライスした図であり、
左右で正解と推定値の2個1組のペアになっています。
いずれの場合も誘電体の場所、形、誘電率が正しく推定できていることがわかります。
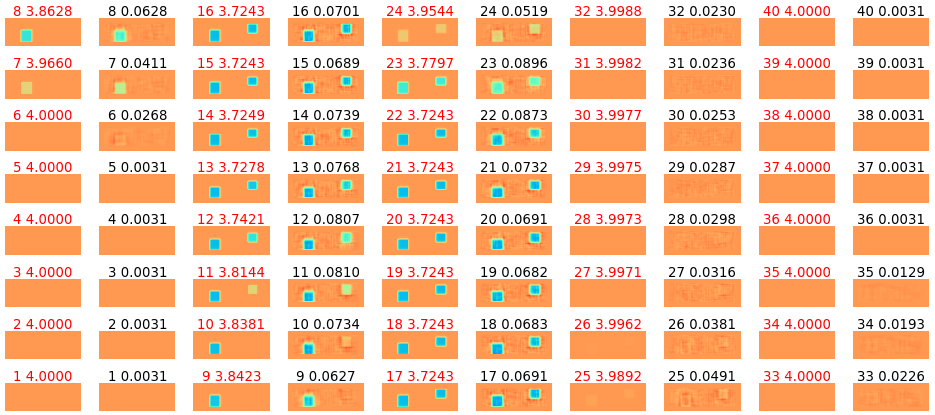

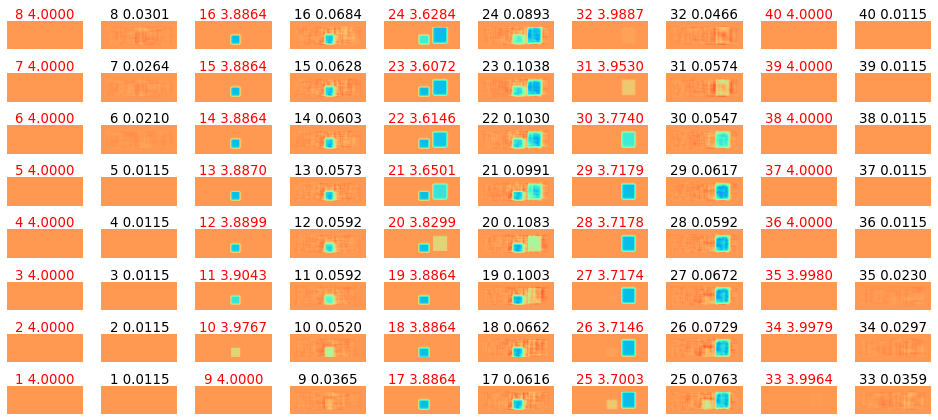
(データ数=10000, ResNet34, Rx-3, ガウスパルス, 112x112px)
図4-9に誘電率分布の推定結果の3D表示を示します。
縦方向に拡大されています。
マウスドラッグで視点を変えることができます。