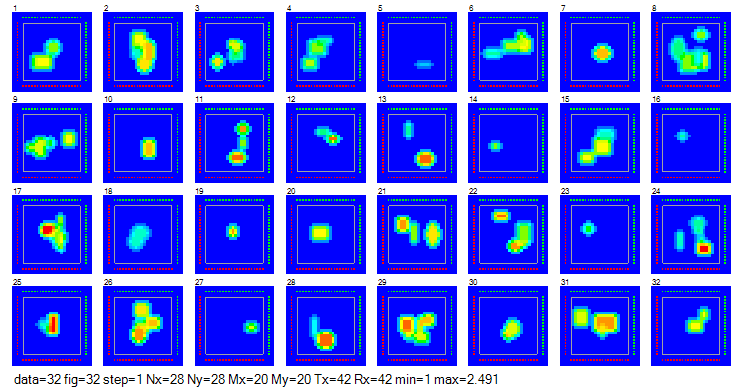
2次元モデルはFDTD法の計算時間が短いために、各種の計算条件を検討することに適しています。
特に断らないときの、FDTD法の計算条件は表3-1の通りです。
| パラメーター | 値 |
|---|---|
| FDTD計算領域のセル数 | Nx=Ny=28 |
| 対象領域(内部領域)のセル数 | Mx=My=20 |
| アンテナ辺数 | 2 |
| 送信アンテナの数 | Tx=42 |
| 受信アンテナの数 | Rx=42 |
| 周波数 | 3.0GHz |
| セルサイズ | Δx=Δy=5mm |
| 送信アンテナの電界方向 | Z方向(紙面に垂直) |
| 受信アンテナの電界方向 | Z方向(紙面に垂直) |
| 給電波形 | 微分ガウスパルス |
| 吸収境界条件 | PML4層 |
| アンテナと内部領域境界の距離 | 2セル |
| タイムステップ数 | 600 |
| データ数 | 20000 |
特に断らないときの、深層学習の計算条件は表3-2の通りです。
| パラメーター | 値 |
|---|---|
| ネットワークモデル | ResNet18, 重みなし |
| 最適化関数 | Adam |
| 入力画素数 | 72x72ピクセル |
| エポック数 | 100 |
| ミニバッチサイズ | 60 |
| 訓練データの割合 | 80% |
| S行列成分 | 実部, 虚部 |
| 誘電率成分 | 実部, 虚部 |
| S行列差分 | あり |
| S行列正規化 | なし |
多数の教師データを作るためには多様な誘電体の集合が必要になります。
表3-3に誘電体のパラメーターと本章で用いた値を示します。
| パラメーター | 値 | 本章の値 |
|---|---|---|
| 誘電体の数 | 指定した範囲内でランダム | 1~5 |
| 誘電体の形状 | 指定した確率で長方形か楕円 | 0.5 |
| 誘電体の位置 | ランダム | |
| 誘電体の大きさ | 指定した範囲内でランダム | 1~8セル |
| 比誘電率 | 指定した範囲内でランダム | 1.5~2.5 |
| 導電率 | 指定した範囲内でランダム | 0.02~0.08[S/m] |
| 誘電率と導電率の平滑化回数 | 固定 | 1 |
| 誘電体位置の平均化個数 | 指定した範囲内でランダム | 2~2 |
| 背景媒質の比誘電率と導電率 | 任意に指定可能 | εr=1, σ=0 (空気) |
●平滑化
誘電率の「平滑化」とは以下の操作を意味します(複数回可能、導電率も同様)。
これによって誘電率の変化が滑らかになります。
εrnew(i,j) = {εr(i,j)+εr(i-1,j)+εr(i+1,j)+εr(i,j-1)+εr(i,j+1)}/5 (3-1)
εr(i,j) = εrnew(i,j)
●平均化
誘電体位置の「平均化」とは複数の乱数の平均をとることを意味します。
これによって誘電体が中央付近に集まる効果があります(大数の法則)。
(1は平均化を行わないことを意味します)
平均化を行うかどうかは推論時のデータの性質によります。
図3-1に教師データの一部の誘電率分布を示します。
青→赤で誘電率が高くなることを表しています。
誘電体がない場所を背景媒質と呼びます。
赤点は送信アンテナ、緑点は受信アンテナです。
導電率分布も同様であり省略します。
教師データから一定の割合(例えば80%)をランダムに選んで訓練データとし、
残りは検証データとします。

アンテナを置く辺数は図3-2のように1辺と2辺が考えられます。
送信アンテナと受信アンテナの数は同じであり、対象領域の反対側に置きます。
アンテナの数は1辺のとき21、2辺のとき42です。
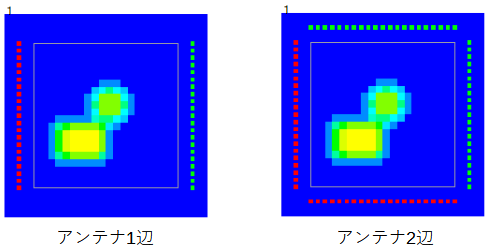
図3-3にアンテナ辺数が1と2のときの損失を示します。
損失は画素数によって変わるために、画素数は同じ条件にしています。
図から2辺のときはより多くの誘電体の情報が得られるために損失が小さくなります。
以下ではアンテナ2辺とします。
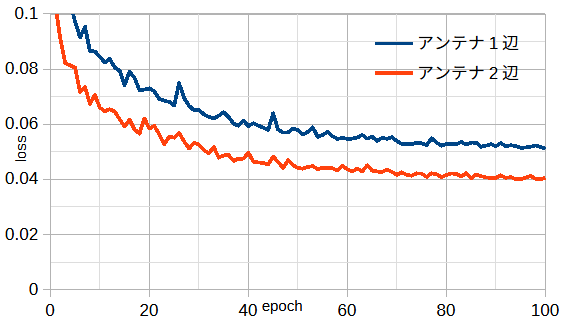
図3-4にS行列差分の方法を示します。
図(a)は通常の方法で求めたS行列です。
図(b)は誘電体がないときのS行列、すなわち送受信アンテナの関係を表します。
図(c)は(a)から(b)を(複素数として)引いたものです。

図3-5にS行列差分がないときとあるときの損失を示すます。
差分をとることによって共通部分が除かれ、精度よく学習できるように思われますが、
図の通り、大きな違いはありません。
深層学習では学習の過程で共通部分は意味のないものとして重みが小さくなり、
自然に無視されるものと思われます。
以下ではS行列差分ありとします。
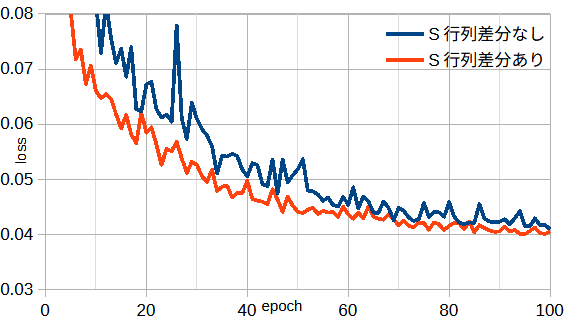
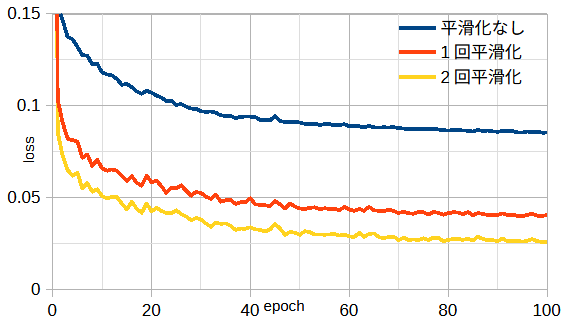
図3-6に平滑化回数と損失の関係を示します。
図から誘電率の平滑化によって損失が小さくなることがわかります。
ただし、平滑化回数は単に大きくすればいいものではなく、
学習の目的は推論を正しく行うことなので、
推論時のデータの誘電率の滑らかさに合わせて学習することが大切です。
なお、FDTD法では誘電体の境界における誘電率は両側の平均を使用します。
すなわち既に平滑化相当の操作が1回行われていることに注意してください。
以下では1回平滑化とします。
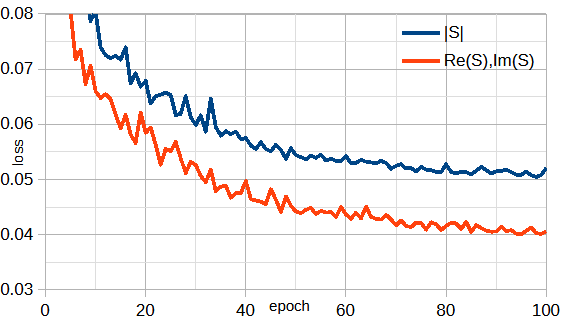
S行列は複素数なので、絶対値をとるか、複素数の実部と虚部をとるかの2通りがあります。
図3-7に両者の比較を示します。
図から複素数の実部と虚部の損失が小さいことがわかります。
複素数の実部と虚部をとるには位相の測定が必要でありコストがかかります。
以下では、S行列は複素数の実部と虚部とします。
誘電率は複素数であり通常は式(2-3)のように実部と虚部の両方から損失を計算しますが、
実部のみまたは虚部のみをとる方法も考えられます。
図3-8に各ケースを比較します。
図から3ケースの収束状況はほぼ同等であることがわかります。
誘電率の成分は計算内部の変数なので、
以下では、情報量の多い誘電率の実部と虚部を使用します。

FDTD法においては1度の計算で複数の周波数の受信電界を求めることができます。
図3-9に1~3個の周波数のS行列を使用したときの損失を示します。
周波数の数が増えるとデータの数が増えることと同じ効果があると期待されますが、
図からは周波数の数を増やす効果は見られません。
以下では1周波数とします。
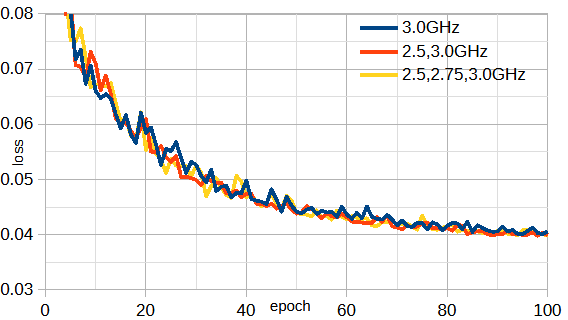
図3-10にネットワークの比較を示します。
一部のネットワークは不安定になります。
1エポック当たりの計算時間はResNet18/34で3.7/6.7秒です。
以下では、性能がよく計算時間も短いResNet18重みなしを使用します。
収束状況は画素数や最適化関数によって変わります。
また、最適なネットワークは問題の大きさ(セル数)やアンテナの数によって変わります。
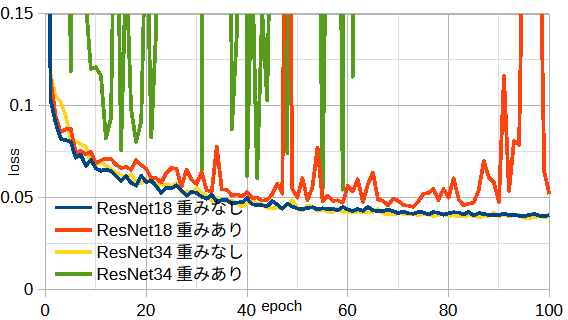
図3-11に最適化関数と損失の関係を示します。
ソースコードの関数名を変えるだけで最適化関数を変えることができます。
図からNAdam以外はほとんど同じです。以下では、Adamを使用します。
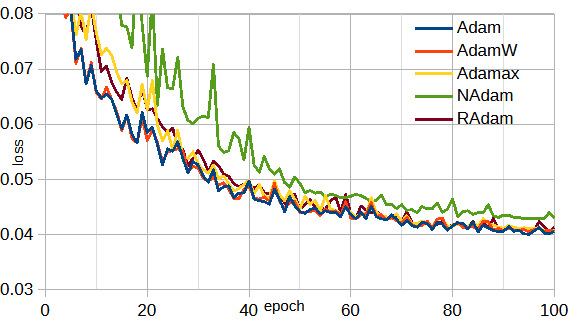
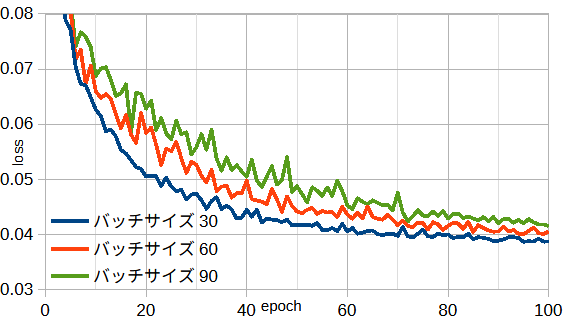
図3-12にミニバッチサイズと損失の関係を示します。
バッチサイズが小さいほど計算時間が増え、
エポックあたりの計算時間はバッチサイズ=30/60/90のとき7.2/3.6/3.3秒です。
使用メモリーはバッチサイズに無関係で2.8GBです。
以下では、計算精度と計算時間を考慮し、
ミニバッチサイズ=60とします。
以下の操作によってS行列(image)を正規化することができます。
正規化することによって測定時の各種因子の影響をなくすことができます。
mean = image.mean() std = image.std() image = (image - mean) / std
図3-13に正規化有無のときの損失を示します。
図から正規化の有無によって損失は変わらないことがわかります。
以下では、正規化なしとします。

ResNetは224x224ピクセルのImageNet向けに学習されているために、
S行列の画素数も224に近い方が精度はよくなりますが、
画素数を増やすと学習時間が増えます。
画素数を変えるにはPyTorchのResize関数を使用します。
図3-14にS行列の画素数と損失の関係を示します。
本ケースでは画素数を増やしても損失はあまり小さくなりません。
エポック当たりの計算時間は画素数=42/72/112のとき3.5/4.2/6.2秒です。
以下では、計算時間と他のケースでの安定性を考慮して72ピクセルとします。
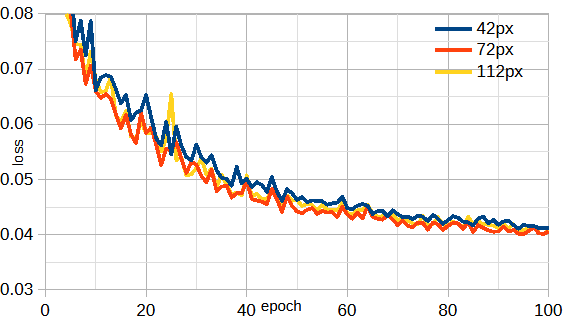
図3-15にデータ数を変えたときの収束状況を示します。
データ数が多いほど損失が小さいことがわかります。
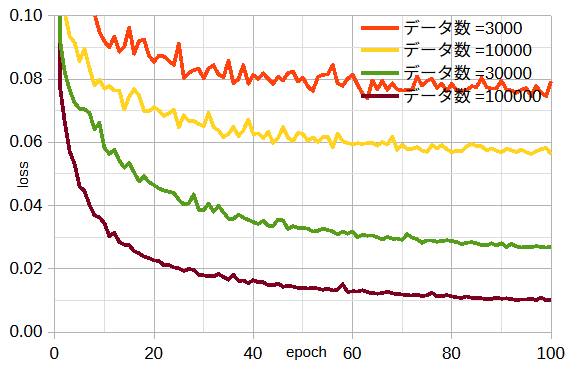
図3-16にデータ数を変えた時の損失の最小値(図3-15の最小値)を示します。
データ数が多いほど損失が小さいことがわかります(スケーリング則)。
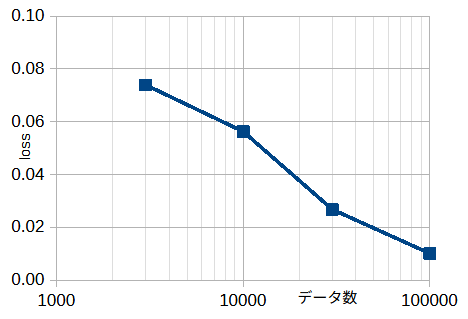
図3-17に15個の検証データについての誘電率分布の推定結果を示します。
上下で正解と推定の2個1組のペアになっています。
すべてのデータについて場所、形、誘電率がほぼ正しく推定できていることがわかります。
上の黒数字は比誘電率の平均、下の赤数字は比誘電率推定誤差の平均です。

図3-18に10個の検証データについて、学習データ数別の誘電率分布を示します。
第1行が正解です。第2行以降は学習データ数を変えたときの推定値です。
これから、学習データ数が多いほど誘電率分布の推定が正確になることがわかります。
ただし学習データ数3000でも大きな誤差はありません。

S行列の測定では測定誤差が避けられません。
ここでは、S行列にランダムな誤差を与えたときの計算結果を見ます。
学習時に、訓練データには誤差を与えずに学習し、
検証データに以下のように正規分布乱数を加えます。
r = 0.1 (S/N比=20dBのとき) image += r * torch.randn(image.shape)
図3-19にS/N比を変えたときの損失を示します。
S/N比が大きくなると損失が小さくなります。
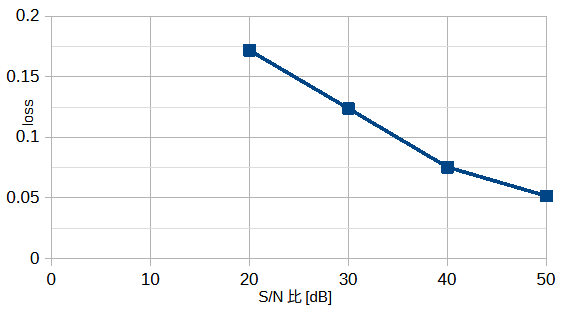
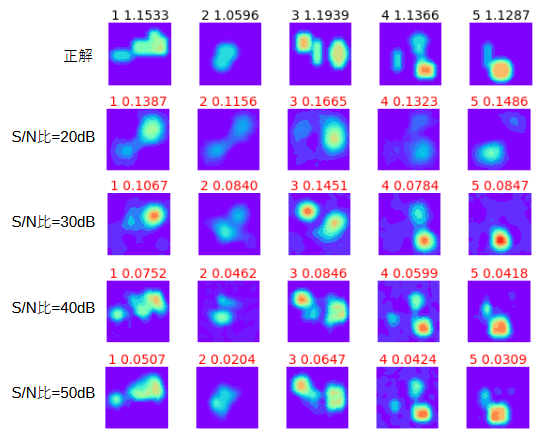
図3-20に5個の検証データをとりあげ、S/N比を変えたときの誘電率分布の推定結果を示します。
色のスケールは共通です。
S/N比が大きくなると推定結果が正確になります。
比誘電率が学習時と異なるデータを推定した結果を調べます。
図3-21に比誘電率(2.5<εr<3.5)の15個のテストデータの推定結果を示します。
学習時の比誘電率は(1.5<εr<2.5)です。
なお、導電率の範囲は学習とテストで同じとしています。
図から、誘電体の場所と形はほぼ正しく推定できますが、
誘電率は学習時の範囲にとどまり低く推定されることがわかります。
これから、実用時の状況を考慮した学習データで学習させることが大切であることがわかります。

周波数が学習時と異なるデータを推定した結果を調べます。
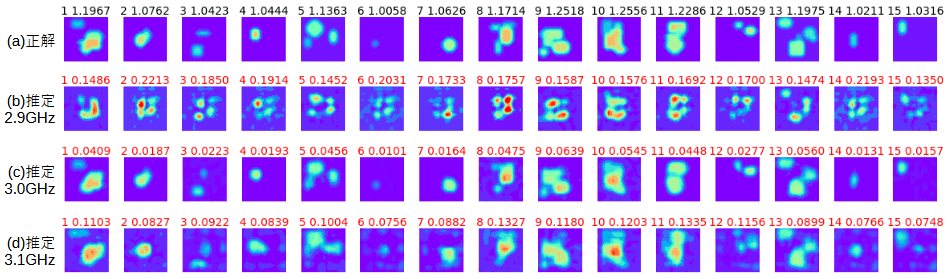
図3-22にS行列作成時(測定時)の周波数を変えたときの15個のテストデータの推定結果を示します。
(a)は正解の誘電率分布です。
(b)(c)(d)は学習時と比べて周波数が低いとき、同じとき、高いときです。
理由は不明ですが、周波数が低いときは推定誤差が大きく、
周波数が高いときは推定誤差が小さくなっています。
アンテナ位置が学習時と異なるデータを推定した結果を調べます。
図3-23にS行列作成時(測定時)のアンテナ位置を学習時から変えたときの15個のテストデータの推定結果を示します。
図中の数字は送信アンテナおよび受信アンテナ位置の対象領域からの距離です。
(a)は正解の誘電率分布です。
(b)は学習時の位置、(c)(d)はそれより5mm/10mm外側に移動したときです。
アンテナ位置が学習時から離れるほど推定誤差が大きくなることがわかります。
