特に断らないときの、FDTD法の計算条件は表4-1の通りです。
| パラメーター | 値 |
|---|---|
| FDTD計算領域のセル数 | Nx=Ny=Nz=28 |
| 対象領域(内部領域)のセル数 | Mx=My=Mz=20 |
| アンテナ面数 | 2 |
| 送信アンテナの数 | Tx=40 |
| 受信アンテナの数 | Rx=40 |
| 周波数 | 3.0GHz |
| セルサイズ | Δx=Δy=Δz=5mm |
| 送信アンテナの電界方向 | Z方向 |
| 受信アンテナの電界方向 | Z方向 |
| 給電波形 | 微分ガウスパルス |
| 吸収境界条件 | PML4層 |
| アンテナと内部領域境界の距離 | 2セル |
| タイムステップ数 | 300 |
| データ数 | 20000 |
特に断らないときの、深層学習の計算条件は表4-2の通りです。
| パラメーター | 値 |
|---|---|
| ネットワークモデル | ResNet18, 重みなし |
| 最適化関数 | Adam |
| 入力画素数 | 72x72ピクセル |
| エポック数 | 100 |
| ミニバッチサイズ | 60 |
| 訓練データの割合 | 80% |
| S行列成分 | 実部, 虚部 |
| 誘電率成分 | 実部, 虚部 |
| S行列差分 | あり |
| S行列正規化 | なし |
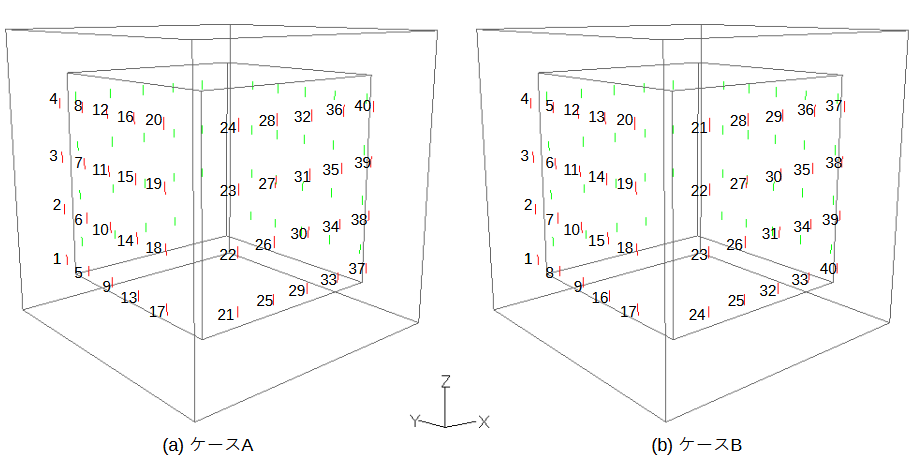
3次元モデルではアンテナを適切に配置することが大切です。
S行列の画像の不連続度が大きくならないように、
アンテナは連続して一筆書きに近い方法で移動させることが望ましいです。
図4-1にアンテナ位置を示します。図中の数字は送信アンテナ番号です。
送信アンテナを-X面と-Y面に置きます。
Z方向の並びについては、(a)では同一方向に、(b)では上下交互に並べます。
同じ番号の受信アンテナを対象領域の反対側に置きます。

図4-2に誘電体がないときのS行列を示します。
誘電体がないときのS行列は送受信間の距離と偏波方向で決まります。
図からS行列には規則的な模様が見られます。
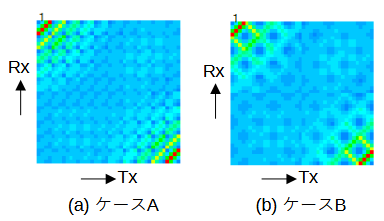
図4-3に誘電体を適当に配置した3データとケースAについて、
(a)にS行列の生データ、(b)に(a)から図4-2(a)を(複素数として)引いたものを示します。
(a)では誘電体の位置によってS行列にごくわずかの差が見られます。
(b)では誘電体の位置の違いが強調されますが、別の規則的な模様が残ります。
ケースBについても同じ傾向が見られます。
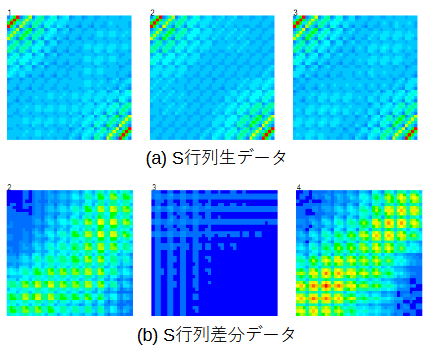
表4-3に誘電体のパラメーターと本章で用いた値を示します。
| パラメーター | 値 | 本章の値 |
|---|---|---|
| 誘電体の数 | 指定した範囲内でランダム | 1~6 |
| 誘電体の形状 | 指定した確率で直方体か楕円体 | 0.5 |
| 誘電体の位置 | ランダム | |
| 誘電体の大きさ | 指定した範囲内でランダム | 1~10セル |
| 比誘電率 | 指定した範囲内でランダム | 1.5~2.5 |
| 導電率 | 指定した範囲内でランダム | 0.02~0.08[S/m] |
| 誘電率と導電率の平滑化回数 | 固定 | 1 |
| 誘電体位置の平均化個数 | 指定した範囲内でランダム | 2~2 |
| 背景媒質の比誘電率と導電率 | 任意に指定可能 | εr=1, σ=0 (空気) |
●平滑化
2次元モデルと同様、以下の誘電率の「平滑化」を考えます(複数回可能、導電率も同様)。
εrnew(i,j,k) = {εr(i,j,k)+εr(i-1,j,k)+εr(i+1,j,k)+εr(i,j-1,k)+εr(i,j+1,k)+εr(i,j,k-1)+εr(i,j,k+1)}/7 (4-1)
εr(i,j,k) = εrnew(i,j,k)
図4-4に1つのデータの誘電率分布を示します。
Z面でスライスした図を順に示しています。
場所、大きさ、誘電率が異なる複数の誘電体が存在することがわかります。
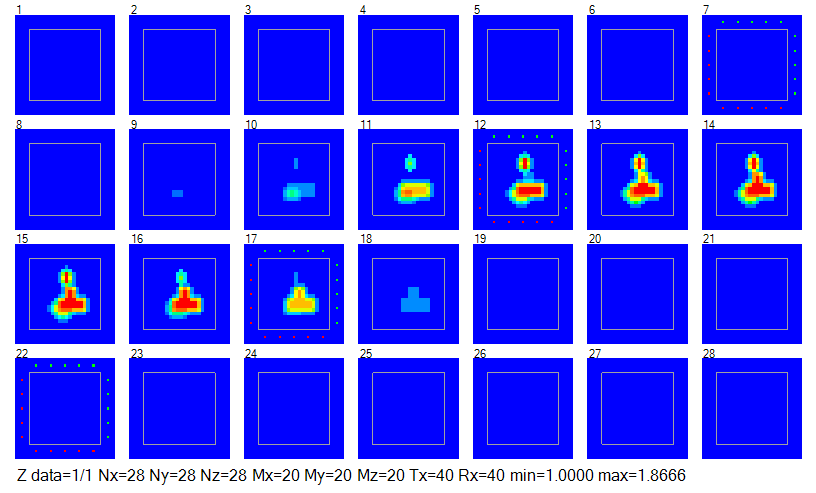
図4-5にS行列差分有無のときの損失を示します。
図からS行列差分ありのときは、損失が小さくなり収束も安定していることがわかります。
以下ではS行列差分ありとします。
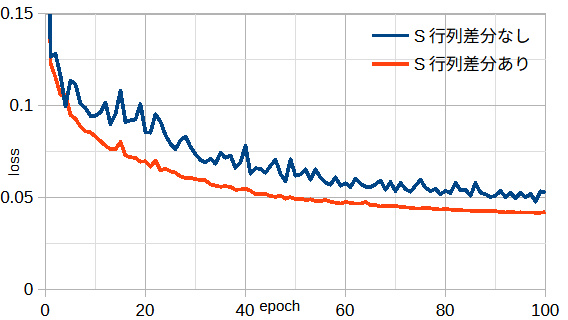
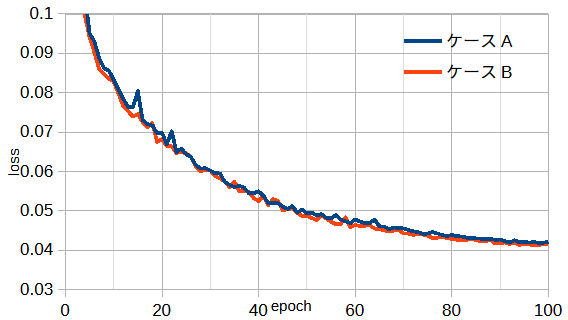
図4-6に図4-1の2つのアンテナ並び順と損失の関係を示します。
両者はほぼ同じですが、以下ではより単純なケースAを考えます。
S行列は複素数なので、絶対値をとるか、複素数の実部と虚部をとるかの2通りがあります。
図4-7に両者の比較を示します。図から両者はほぼ同じです。
以下では、S行列は複素数の実部と虚部とします。
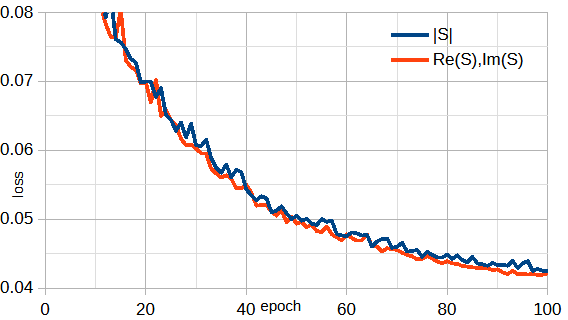
図4-8にS行列の画素数と損失の関係を示します。
安定的に収束するにはある程度以上の画素数が必要であることがわかります。
エポック当たりの計算時間は画素数=40/56/72/112ピクセルのとき5.7/5.8/6.6/8.6秒です。
使用メモリーは画素数=40/56/72/112ピクセルのとき5.1/5.4/5.7/7.0GBです。
以下では、安定性、計算時間、計算精度を考慮して画素数=72ピクセルとします。

図4-9にネットワークの比較を示します。
ResNet34重みなしは不安定ですが、それ以外はほぼ同等です。
1エポック当たりの計算時間はResNet18/34で6.2/9.2秒です。
使用メモリーはネットワークによらず5.7GBです。
以下では、性能がよく計算時間も短いResNet18重みなしを使用します。
最適なネットワークは問題の大きさ(セル数)やアンテナの数によります。
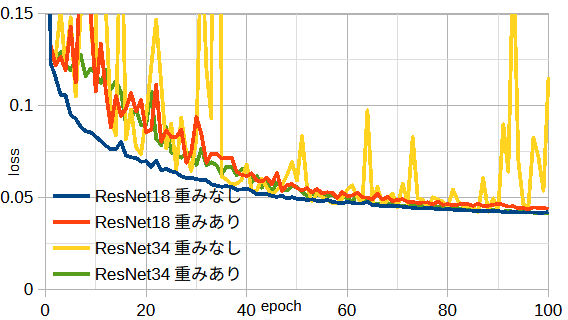
図4-10にデータ数を変えたときの収束状況を示します。
2次元モデルと同じく、データ数が多いほど損失が小さくなることがわかります。
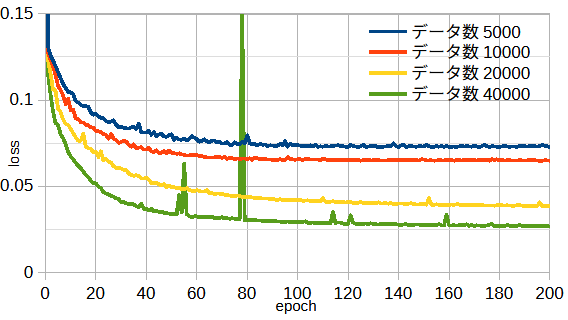
図4-11にデータ数を変えた時の損失の最小値(図4-10の最小値)を示します。
データ数が多いほど損失が小さくなることがわかります。
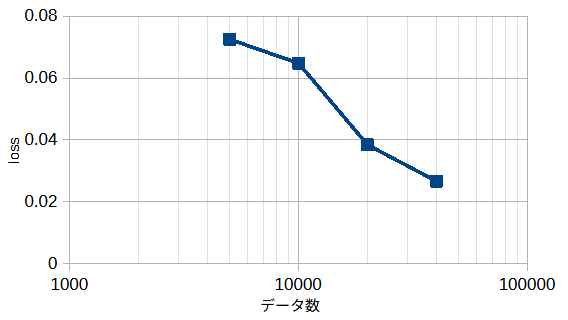
図4-12に5個の検証データの誘電率分布の推定結果を示します。
Z面(全20面)についてスライスした図であり、
上下で正解と推定の2個1組のペアになっています。
すべてのデータについて場所、形、誘電率がほぼ正しく推定できていることがわかります。

(a)データ#1

(b)データ#2

(c)データ#3

(d)データ#4

(e)データ#5