数値ファントムはボクセル数=100x100x50、分解能=1mmですが、
このままではデータ量が多いので、分解能Dを大きくしています。
D3個のボクセルを合体して1個のセルとしています。
その誘電率は各ボクセルの誘電率の平均です。
FDTD法の計算条件は表3-1の通りです。
| パラメーター | 値 |
|---|---|
| セルサイズ(分解能) | D=Δx=Δy=5mm |
| 対象領域(内部領域)のセル数 | Mx=My=20 |
| 外部領域のセル数 | 4 |
| FDTD計算領域のセル数 | Nx=Ny=28 |
| 送信アンテナの数 | Tx=42(-X面, -Y面) |
| 受信アンテナの数 | Rx=42(+X面, +Y面) |
| 周波数 | 2.0GHz |
| 送信アンテナの電界方向 | Z方向(紙面に垂直) |
| 受信アンテナの電界方向 | Z方向(紙面に垂直) |
| 給電波形 | 微分ガウスパルス |
| 吸収境界条件 | PML4層 |
| アンテナと内部領域境界の距離 | 2セル |
| タイムステップ数 | 600 |
| データ数 | 20000 |
深層学習の計算条件は表3-2の通りです。
| パラメーター | 値 |
|---|---|
| ネットワークモデル | ResNet18, 重みなし |
| 最適化関数 | Adam |
| 入力画素数 | 72x72ピクセル |
| エポック数 | 100 |
| ミニバッチサイズ | 60 |
| 訓練データの割合 | 80% |
| S行列成分 | 実部, 虚部 |
| 誘電率成分 | 実部, 虚部 |
| S行列差分 | あり |
| S行列正規化 | なし |
多数の教師データを作るためには多様な誘電体の集合が必要になります。
表3-3に誘電体のパラメーターと本章で用いた値を示します。
| パラメーター | 値 | 本章の値 |
|---|---|---|
| 誘電体の数 | 指定した範囲内でランダム | 2~10 |
| 誘電体の形状 | 指定した確率で長方形か楕円 | 0.5 |
| 誘電体の位置 | ランダムただし半径50mm内に限定 | |
| 誘電体の大きさ | 指定した範囲内でランダム | 1~6セル |
| 誘電率と導電率の平滑化回数 | 固定 | 1 |
| 誘電体位置の平均化個数 | 指定した範囲内でランダム | 1~3 |
| 乳腺とがんの比 | 指定した確率でランダム | 8:2 |
| テストデータの形状 | case1~3のZ断面の下から30面(1mm間隔) | |
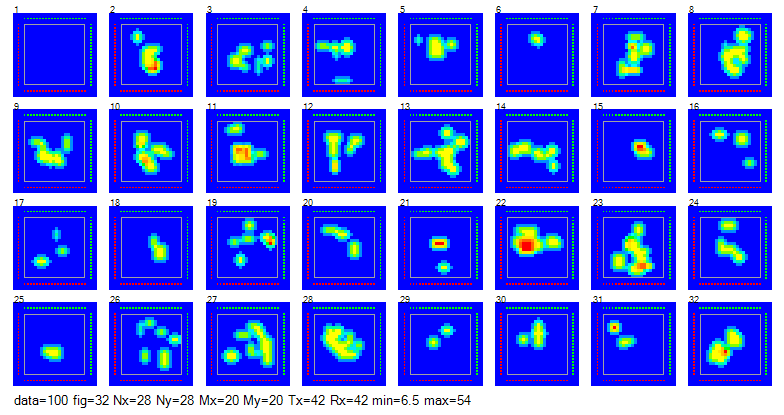
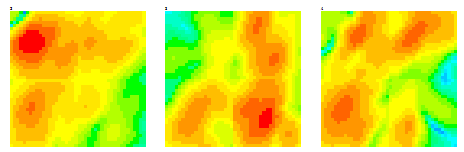
図3-1に教師データの一部の誘電率分布を示します。
誘電体は内部領域に置かれます。
青→赤で誘電率が高くなることを表しています。
乳腺とがん以外はすべて脂肪とします。
がんが赤、乳腺が黄、脂肪が青ですが、
ボクセルの合体と平滑化を行っているために中間色もあります。
赤点は送信アンテナ、緑点は受信アンテナです。
導電率分布も同様であり省略します。

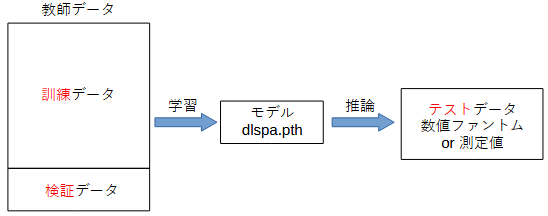
図3-2に訓練(train)、検証(validation)、テスト(test)データの関係を示します。
教師データから一定の割合(例えば80%)をランダムに選んで訓練データとして学習します。
学習中に検証データの損失を出力して収束状況を確認します。
学習によって得られたモデルを用いて、
教師データとは異なるデータ(ここでは数値ファントム)でテストしてモデルの性能を評価します。
モデルの性能は式(3-1)のテスト誤差で評価します。
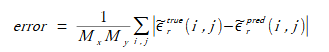 (3-1)
(3-1)
図3-3(a)に3個のデータのS行列を示します。
送受信アンテナの位置関係に起因する共通の模様が見られ、
本来の誘電体による影響が小さくなります。
(b)は第1データを誘電体のない状態とし、
第2データ以降のS行列から第1データのS行列を(複素数として)引いたものです。
(b)では誘電体の差が強調されるので学習の精度が上がることが期待されます。
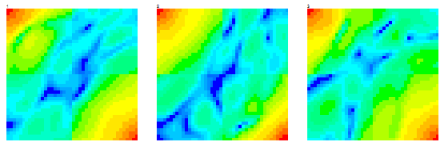
(a) S行列の生データ
(b) 差分後のS行列
図3-4にS行列について、絶対値/複素数、差分あり/なしのときの損失を比較します。
図から、複素数をとったとき損失が小さくなりますが、差分の影響は小さいことがわかります。
以下では、差分あり複素数とします。
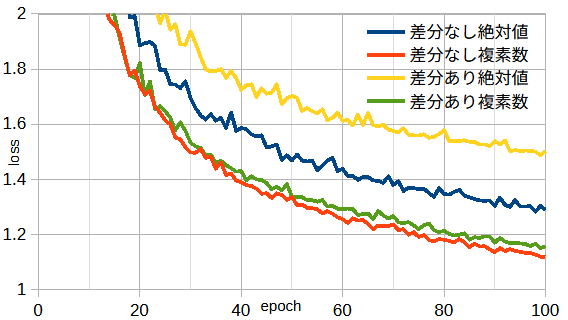
図3-5にネットワークの比較を示します。
ResNet34はResNet18よりわずかに損失が小さくなります。
1エポック当たりの計算時間はResNet18/34で4.0/7.3秒です。
必要なネットワークの深さは問題の大きさと難しさによります。
以下では、ResNet18重みなしを使用します。

S行列の画素数はアンテナの数と一致します。
学習の前処理で画素数を変えることができます。
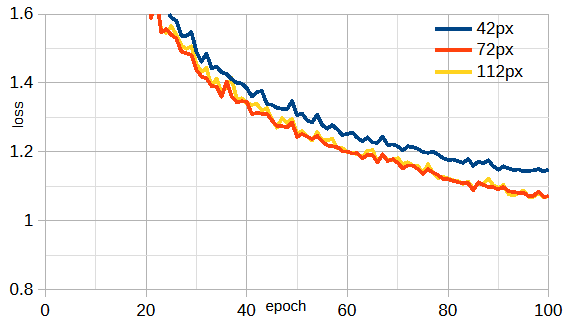
図3-6に画素数と損失の関係を示します。
画素数=42のみ少し損失が大きくなっています。
1エポック当たりの計算時間は画素数=42/72/112のとき3.5/4.0/6.2秒です。
画素数が小さいときは収束が不安定になることがあります。
必要な画素数は問題の大きさと難しさによります。
以下では、画素数=72ピクセルとします。
以下の操作によってS行列(image)を正規化することができます。
正規化することによって測定時の各種因子の影響をなくすことができます。
mean = image.mean() std = image.std() image = (image - mean) / std
図3-7に正規化有無のときの損失を示します。
図から正規化の有無によって損失は変わらないことがわかります。
以下では、正規化なしとします。

図3-8にデータ数を変えたときの収束状況を示します。
データ数が多いほど損失が小さいことがわかります。
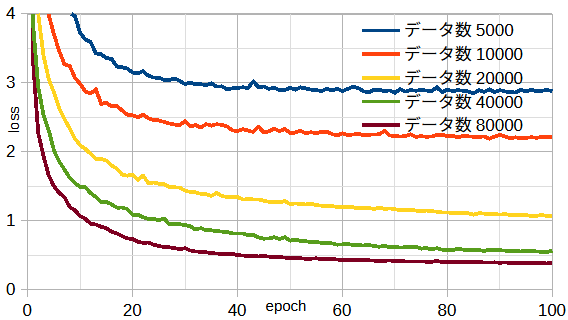
図3-9にデータ数を変えた時の損失の最小値(図3-8の最小値)を示します。
データ数が多いほど損失が小さいことがわかります(スケーリング則)。

図3-10に15個の検証データの誘電率分布の推定結果を示します。
上下で正解と推定の2個1組のペアになっています。
複素比誘電率の絶対値を表示しています。
色のスケールは共通(|εr|=5~55)です。
上の黒数字は比誘電率の平均、下の赤数字は比誘電率推定誤差の平均です。
すべてのデータについて場所、形、誘電率がほぼ正しく推定できていることがわかります。

数値ファントムの誘電率を推定します。これが最終的な目的です。
分解能をD=5,4,3mmと変え、計算条件も表3-4のように変えます。
表3-4にない項目は表3-1~表3-3と同じです。
| 分解能 | D=5mm | D=4mm | D=3mm |
|---|---|---|---|
| 対象領域のセル数, Mx=My | 20 | 25 | 33 |
| FDTD計算領域のセル数, Nx=Ny | 28 | 33 | 41 |
| 送信アンテナの数, Tx | 42 | 52 | 68 |
| 受信アンテナの数, Rx | 42 | 52 | 68 |
| データ数 | 40000 | ||
| ネットワークモデル | ResNet34, 重みなし | ||
| 入力画素数 | 112x112ピクセル | ||
| エポック数 | 200 | ||
| 誘電体の数 | 2~10 | ||
| 誘電体の大きさ | 1~6セル | 1~8セル | 1~10セル |
図3-11~図3-13にcase1~3の分解能D=5~3mmの結果を示します。
それぞれ2mm間隔の計15個のZ断面のテストデータの誘電率分布の推定結果です。
上下で正解と推定の2個1組のペアになっています。
複素比誘電率の絶対値を表示しています。
色のスケールは共通(|εr|=5~55)です。
図中の赤い所ががんです。図中の「誤差」は全30面の平均誤差です。
すべてのケースについて場所、形、誘電率がほぼ正しく推定できていることがわかります。
解像度Dによる違いは大きくありませんが、
解像度が小さくなると推定の形状がより正確になる傾向は確認できます。
解像度が小さくなると正解の不連続度が大きくなるために図中の「誤差」は大きくなります。

(a) D=5mm (誤差=1.4690)

(b) D=4mm (誤差=1.6996)

(c) D=3mm (誤差=1.9556)

(a) D=5mm (誤差=1.8766)

(b) D=4mm (誤差=1.9811)

(c) D=3mm (誤差=2.3027)

(a) D=5mm (誤差=1.4718)

(b) D=4mm (誤差=1.7930)

(c) D=3mm (誤差=1.9591)
図3-14にcase1~3のがんがあるときとないときの推定結果を比較します。
分解能D=3mmとしています。がんを通る3mm間隔の4個のZ断面をとっています。
左ががんがあるとき、右ががんがないとき(がんをすべて乳腺に置き換えたもの)です。
複素比誘電率の絶対値を表示しています。
色のスケールは共通(|εr|=5~55)です。
case1とcase2については、がんが約20mmと大きいためにがんの有無が判定できます。
case3については、がんが約10mmと小さいためにがんの有無が判定できません。

図3-15にcase1~3の推定の比誘電率分布のヒストグラムを示します。
横軸は比誘電率、縦軸は頻度です。
case1とcase2ではがんがあるとき誘電率の高い方に裾野が広がりがんが判定できます。
case3ではがんの有無で違いは見られずがんは判定できません。
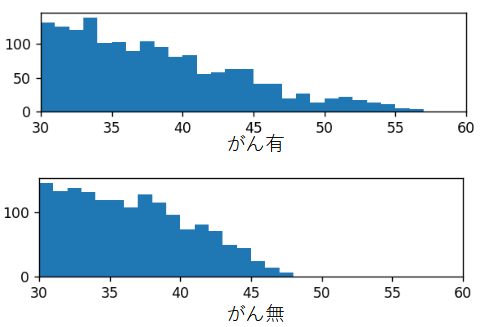
(a) case1
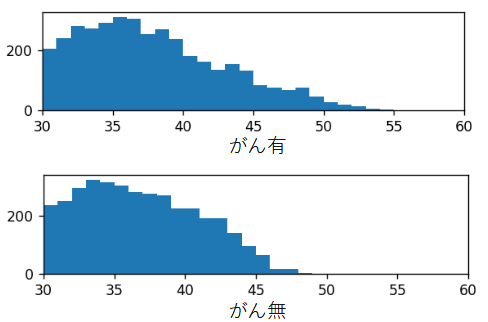
(b) case2

(c) case3