2. 計算手法

2.1 処理の流れ

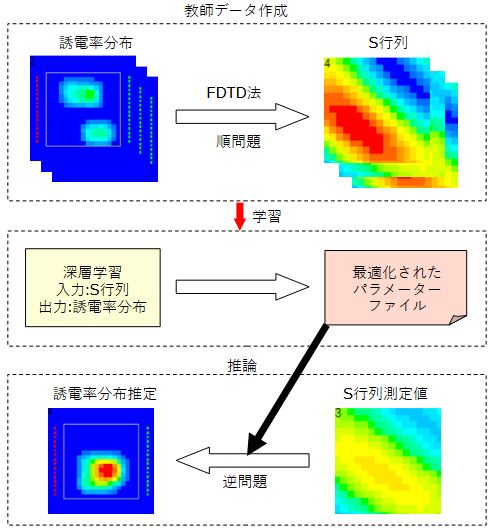
図2-1に処理の流れを示します。
以下の三つの部分から成ります。

教師データ作成: 多数の誘電率分布を作成し、FDTD法によりS行列を計算します。
学習: 深層学習により教師データを学習し、最適化されたパラメーターファイルファイルを得ます。
推論: パラメーターファイルファイルを用いてS行列測定値から誘電率分布を推定します。

2.2 FDTD法

図2-2にFDTD法の計算モデルを示します。
誘電体を含む対象領域を考え、その外部に送信アンテナと受信アンテナを置きます。それらを含む領域がFDTD法の計算領域となり、計算領域の電界分布が計算されます。
3次元モデルではZ方向について同様に考えます。アンテナの配置については後述します。

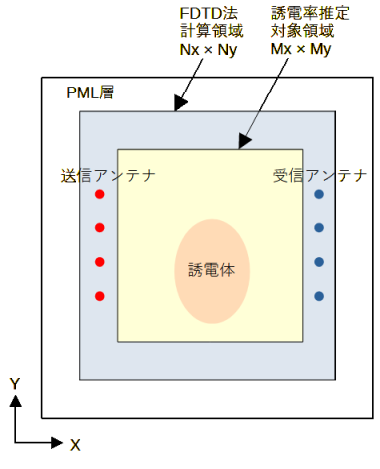
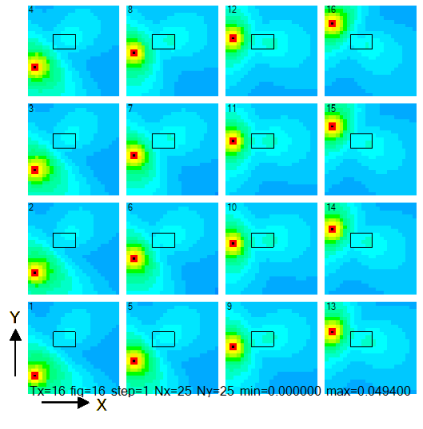
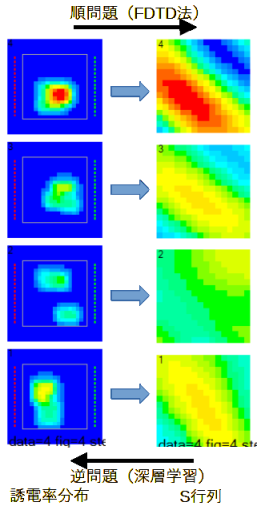
図2-3に送信アンテナを移動させたときの電界分布を示します。
送信アンテナの数は16です。図中の赤い点が送信アンテナであり、黒い線が誘電体です。
送信アンテナを移動させると電界分布が変わります。誘電体は電界を集める効果があります。

FDTD法では一つの送信アンテナを給電すると、すべての受信アンテナの電界を一度に求めることができます。
したがって図2-3の計算から図2-4のようなS行列が得られます。
ここで横軸は送信アンテナ、縦軸は受信アンテナです。
S行列は誘電率分布の情報を持っています。

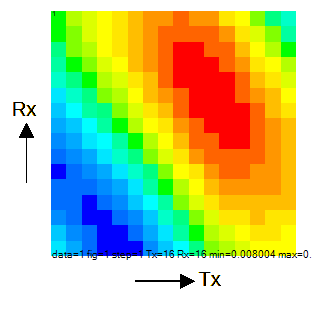
図2-5に順問題と逆問題の関係を示します。
上で述べた方法により誘電率分布からS行列を求めることが順問題です。
逆にS行列から誘電率分布を求めることが逆問題であり、本プログラムの目的です。

2.3 深層学習

前項の方法で誘電体分布をランダムに変えて計算し、多数の誘電体分布とS行列の組（教師データ）を求めます。
そのデータを用いて深層学習を行い、S行列から誘電率分布を推定することを考えます。
図2-6と図2-7にネットワークモデルを示します。図2-6は通常のCNN（畳み込みニューラルネットワーク）、図2-7はResNet[4]です。ResNetでは加算(shortcut connections)が加わります。

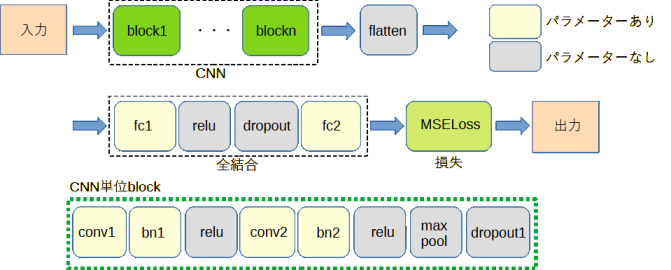
図2-6、図2-7において、「入力」はS行列画像のピクセル値、「出力」は次式で計算される損失(MSELoss)です。
ここで、(Mx, My, Mz)は対象領域のセル数、 ε_r^trueは正解（教師データ）の比誘電率、 ε_r^predは比誘電率の予測値です。
以下では、"損失(loss)"は式(2-2)とします。これは比誘電率の予測誤差の平均値を表します。

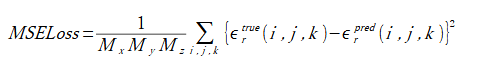　(2-1)
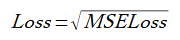　(2-2)

リスト2-1に学習部のソースコードを示します。
ユーザーの行う作業は以下の2点です。

S行列と誘電率分布の教師データをdatasetに代入する
図2-6または図2-7のモデルを記述する

その他は深層学習共通のコードです。

リスト2-1 学習部のソースコード(PyTorch)

dataset設定      ※
dataloader設定
model設定        ※
criterion = nn.MSELoss()                      # 損失関数: MSE
optimizer = optim.Adam(model.parameters())    # 最適化関数: Adam
for epoch in range(num_epochs):               # エポックに関するループ
    for data, target in train_loader:         # ミニバッチに関するループ
        optimizer.zero_grad()                 # 勾配初期化
        output = model(data)                  # 順伝搬
        loss = criterion(output, target)      # 損失計算
        loss.backward()                       # 逆伝搬
        optimizer.step()                      # 最適化関数更新

リスト2-2にResNetのソースコードを示します。
ブロック数とチャンネル数を引数で指定することができます。

リスト2-2 ResNetのソースコード(PyTorch)

import torch
from torch import nn

class BasicBlock(nn.Module):

    def __init__(self, channels, dropout):
        super().__init__()

        self.conv1    = nn.Conv2d(channels, channels, kernel_size=3, stride=1, padding=1, bias=False)
        self.bn1      = nn.BatchNorm2d(channels)
        self.relu     = nn.ReLU(inplace=True)
        self.conv2    = nn.Conv2d(channels, channels, kernel_size=3, stride=1, padding=1, bias=False)
        self.bn2      = nn.BatchNorm2d(channels)
        self.dropout1 = nn.Dropout(dropout)

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        out = self.conv1(x)
        out = self.bn1(out)
        out = self.relu(out)
        out = self.conv2(out)
        out = self.bn2(out)
        out += x  # ResNet
        out = self.relu(out)
        out = self.dropout1(out)

        return out

class ResNet(nn.Module):

    def __init__(self, in_filters, num_blocks, channels, dropout, out_classes):
        super().__init__()

        self.conv1    = nn.Conv2d(in_filters, channels, kernel_size=3, stride=1, padding=1, bias=False)
        self.bn1      = nn.BatchNorm2d(channels)
        self.relu     = nn.ReLU(inplace=True)
        self.maxpool  = nn.MaxPool2d(2, ceil_mode=True)
        self.dropout1 = nn.Dropout(dropout)

        self.blocks   = nn.Sequential(*[BasicBlock(channels, dropout) for _ in range(num_blocks)])

        self.avgpool  = nn.AdaptiveAvgPool2d(1)
        self.flatten  = nn.Flatten()
        self.fc       = nn.Linear(channels, out_classes)

    def forward(self, x):
        x = self.conv1(x)
        x = self.bn1(x)
        x = self.relu(x)
        x = self.maxpool(x)
        x = self.dropout1(x)

        x = self.blocks(x)

        x = self.avgpool(x)
        x = self.flatten(x)
        x = self.fc(x)

        return x