3. 2次元モデルの計算

3.1 計算条件

FDTD法の計算条件は以下の通りです。

• 計算領域のセル数: Nx=Ny=25
• 対象領域のセル数: Mx=My=17
• 送信アンテナの数: Tx=16
• 受信アンテナの数: Rx=16
• 周波数: 3.0GHz
• セルサイズ: Δx=Δy=5mm
• 送信アンテナの電界方向: Z方向（紙面に垂直）
• 受信アンテナの電界方向: Z方向（紙面に垂直）
• 給電波形: 微分ガウスパルス
• 吸収境界条件: PML6層
• タイムステップ数: 600

深層学習の計算条件は以下の通りです。

• ネットワークモデル: ResNet, 5ブロック, 256チャンネル一定, dropoutなし
• 最適化関数: Adam
• ミニバッチサイズ: 50

3.2 誘電率分布

多数の教師データを作るためには多数の異なる誘電率分布が必要になります。
ここでは場所、大きさ、比誘電率（1.5<ε_r<2.5）、 導電率（0.02<σ<0.08[S/m]）をランダムにとった3個の長方形の集合を考えます。
さらに、誘電率を滑らかに変化させるために以下の5点平均化を2回行っています（導電率も同様）。

ε_r(i,j) ← {ε_r(i,j)+ε_r(i-1,j)+ε_r(i+1,j)+ε_r(i,j-1)+ε_r(i,j+1)}/5

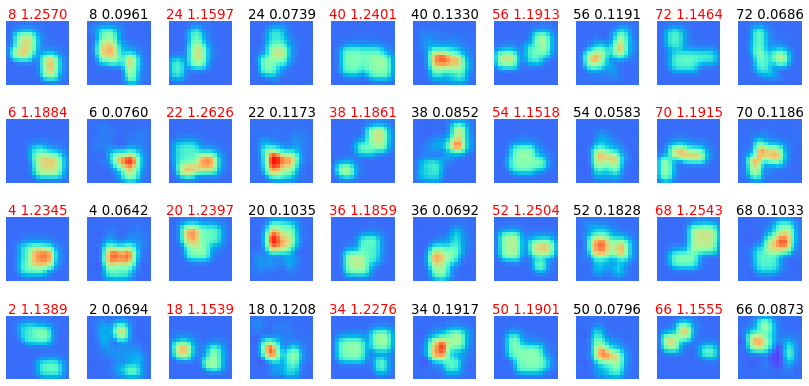
図3-1に教師データの誘電率分布の一部を示します。
青→赤で誘電率が高くなることを表しています。 誘電体がない場所（背景媒質）は空気（ε_r=1,σ=0）としています（変更可能）。
教師データから一定の割合（例えば80%）をランダムに選んで訓練データとし、 残りは検証のためのテストデータとします。

3.3 データ数についての考察

図3-2にデータ数を変えたときの収束状況を示します。
データ数が多いほど最終的な損失が小さいだけでなく収束も安定してかつ速いことがわかります。

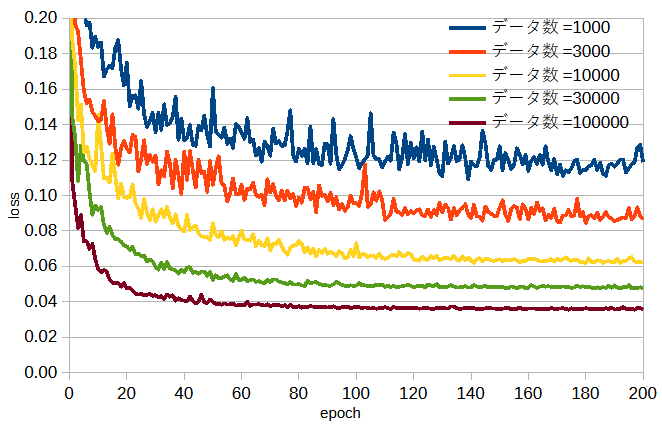
図3-3にデータ数を変えた時の損失の最小値（図3-2の最小値）を示します。
データ数が多いほど損失が小さくなることがわかります。

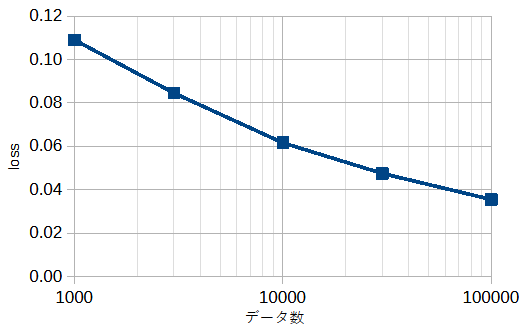
図3-4に4つのデータに選んで誘電率分布図を示します。
左端が正解です。上の赤い数値は比誘電率の平均です。
右の5列はデータ数を変えたときの誘電率分布の推定値です。 上の黒い数値は比誘電率の平均誤差です。
これから、データ数が多いほど誘電率分布の推定が正確になることがわかります。
ただしデータ数1000でも大きな誤差はありません。

3.4 誘電率分布の推定結果

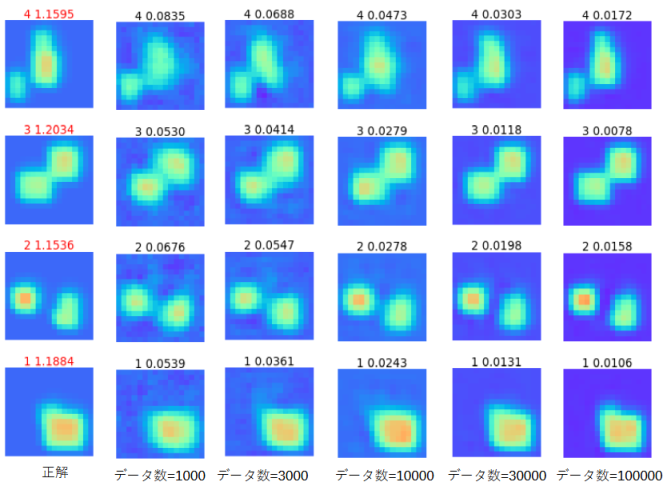
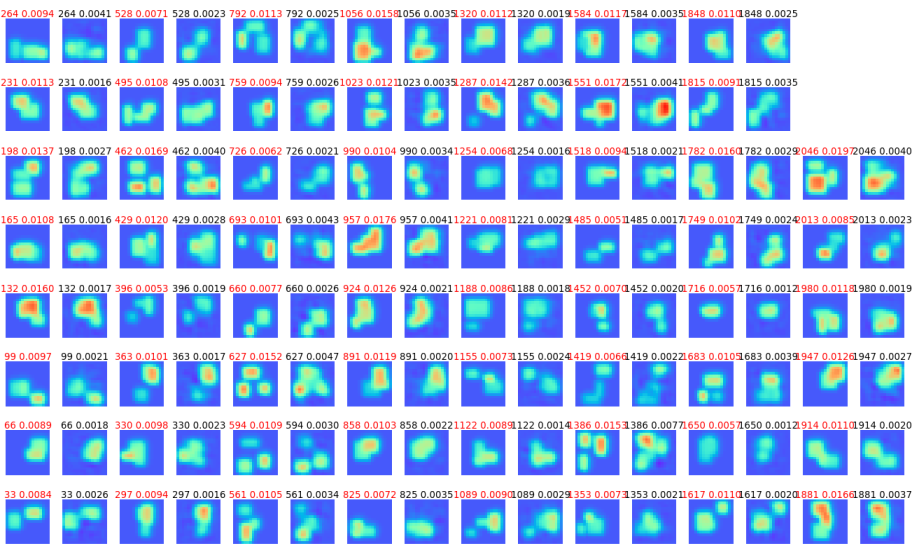
図3-5に63個のデータについて誘電率分布の推定結果を示します。
左右で正解と推定値の2個1組のペアになっています。
すべてのデータについて場所、形、誘電率が正しく推定できていることがわかります。

3.5 ネットワークモデルの比較

図3-6にネットワークモデルの比較を示します。
ResNetは標準のCNNより少し勝ります。
本プログラムではResNetを用いて計算します。

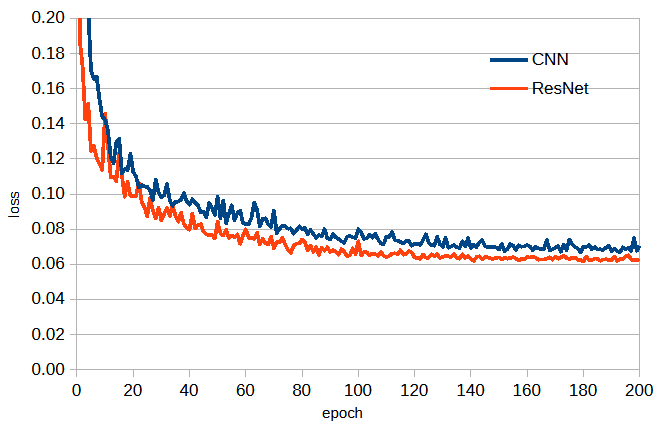
図3-7にResNetにおいてブロック数とチャネル数を変えた時の損失を示します。
ブロック数とチャネル数を増やすと損失が小さくなります。 ただし、ブロック数5と6はほぼ同じです。

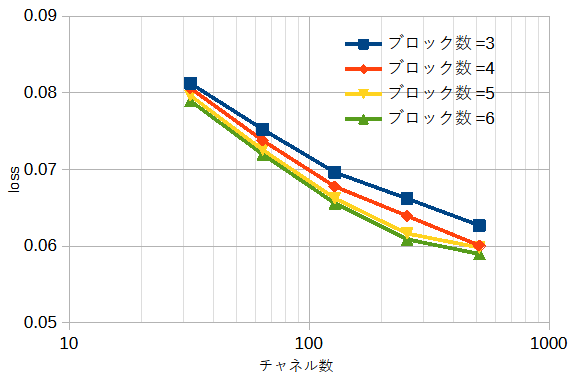
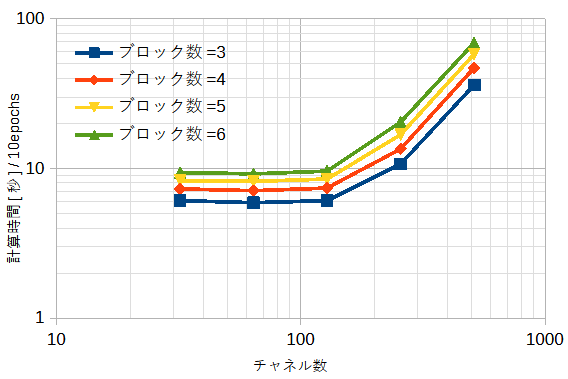
図3-8に図3-7の計算時間を示します。 チャネル数32～128で計算時間はほぼ一定ですが、 それを超えると計算時間が増えます。
本プログラムでは計算精度と計算時間を考慮してブロック数=5、チャネル数=256とします。

3.6 S行列の位相の利用

受信電界は振幅と位相を持つ複素数であるためにS行列も複素数になります。
表3-1にS行列の振幅のみを使用するときと、実部と虚部を使用するときのlossを示します。
これから、位相を利用したほうがlossが少し小さくなることがわかりますが、 位相の測定はコストがかかるので、本プログラムでは振幅のみを考えます。

3.7 導電率分布の推定

図3-9に導電率分布の推定結果を示します。
図3-5の誘電率と比べてデータ数は少ないが遜色ない結果が得られています。
ただし、本プログラムでは誘電率のみを考えます。

3.8 学習対象外のデータの推定

以上の学習では、誘電率が滑らかに変化する3個の長方形の集合で学習しました。
その学習パラメーターで誘電率が不連続に変化する1個の長方形のテストデータを推定した結果を図3-10に示します。
境界は滑らかになりすすが、 誘電体の場所、形、誘電率がほぼ正しく推定できていることがわかります。

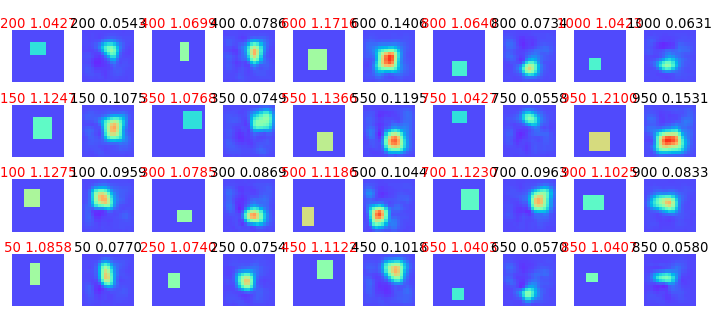
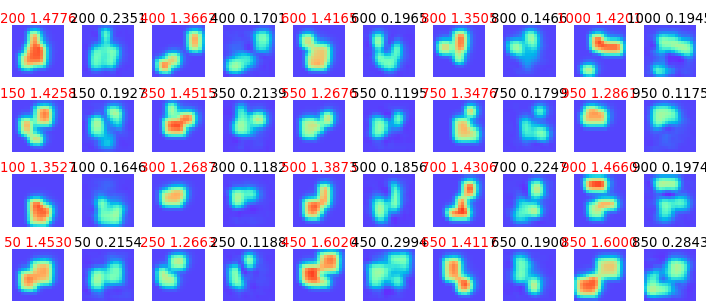
図3-11に学習時の比誘電率（1.5<ε_r<2.5） と異なる比誘電率（2.5<ε_r<3.5）のテストデータを推定した結果を示します。
誘電体の場所と形はほぼ正しく推定できますが、誘電率は正しく推定できません。
これから、実用時の状況を考慮した学習データで学習させることが大切であることがわかります。

3.9 S行列のノイズの影響

S行列の測定では測定誤差が避けられません。 ここでは、S行列が誤差を持つときに誘電率を推定します。
Pythonでテストデータに以下のように正規分布する乱数を加えます。

image += 0.1 * np.random.standard_normal(image.shape)　　(S/N比=20dBのとき)

図3-12にS/N比を変えたときのlossを示します。 S/N比が大きくなるとlossが小さくなります。

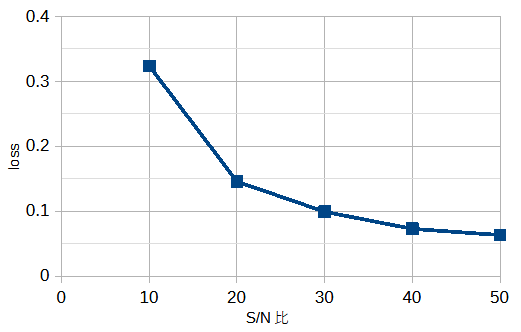
図3-13に4個のデータをとりあげ、S/N比を変えたときの誘電率分布の推定結果を示します。 色のスケールは共通です。
S/N比が大きくなると推定結果が正確になります。 図からS/N比は20～30dBは必要と思われます。

3.10 周波数が異なるデータの推定

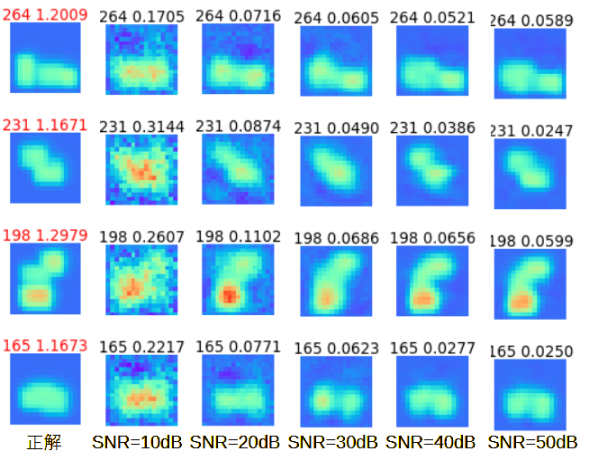
図3-14に3GHzで学習したモデルで2.7GHzのS行列を推定した結果を示します。
周波数が変わればS行列も変わりますが、 図から比較的正しく誘電率分布が推定できていることがわかります。 これは深層学習の汎化性能(Generalization Performance)を表しています。 学習時と異なる条件で得られたデータにも対応することができ、 測定時の各種の測定誤差に対応できることを示唆しています。

3.11 アンテナ位置が異なるデータの推定

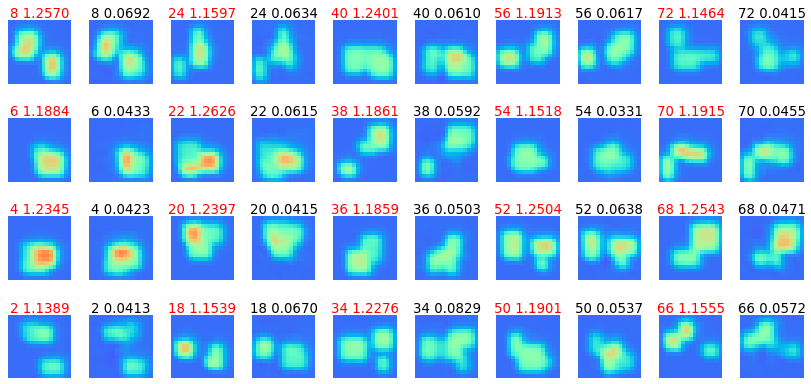
図3-15に送受信アンテナ間を4セル(2cm)離して取得したデータ（S行列）を推定した結果を示します。
図から比較的正しく誘電率分布が推定できていることがわかります。 これも前項と同じく深層学習の汎化性能を表しています。