4. 3次元モデルの計算

4.1 アンテナ位置

3次元モデルではアンテナを適切に配置することが大切です。
S行列の画像が不連続にならないように、 アンテナは連続して一筆書きで移動させることが望ましいです。
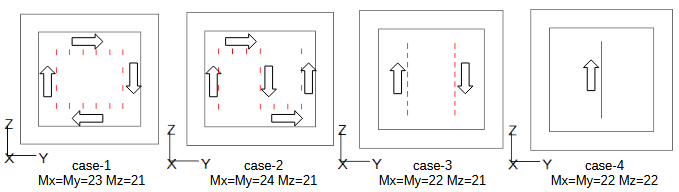
図4-1に4つのケースのアンテナ位置を示します。 アンテナを矢印の方向に移動させます。 アンテナ数は16で共通です。 送信アンテナを-X面境界に置き、受信アンテナを+X面境界の同じ位置に置きます。

図4-2に誘電体がないときの各ケースのS行列を示します。各ケースの色スケールは共通です。
このときのS行列は送受信間の距離と偏波方向で決まります。
図から送受信アンテナ間の位置関係から規則的な模様が見られます。

4.2 計算条件

FDTD法の計算条件は以下の通りです。

• 計算領域のセル数: Nx=Mx+8, Ny=My+8, Nz=Mz+8
• 送信アンテナの数: Tx=16
• 受信アンテナの数: Rx=16
• 周波数: 3.0GHz
• セルサイズ: Δx=Δy=Δz=5mm
• 送信アンテナの電界方向: Z方向
• 受信アンテナの電界方向: Z方向
• 給電波形: 微分ガウスパルス
• 吸収境界条件: PML6層
• タイムステップ数: 300

深層学習の計算条件は以下の通りです。

• ネットワークモデル: ResNet, 5ブロック, 256チャンネル一定, dropoutなし
• 最適化関数: Adam
• ミニバッチサイズ: 50

4.3 誘電率分布

場所、大きさ、比誘電率（1.5<ε_r<2.5）、 導電率（0.02<σ<0.08[S/m]）をランダムにとった2個の直方体の集合を考えます。
さらに、誘電率を滑らかに変化させるために以下の7点平均化を2回行っています（導電率も同様）。

ε_r(i,j,k) ← {ε_r(i,j,k)+ε_r(i-1,j,k)+ε_r(i+1,j,k)+ε_r(i,j-1,k)+ε_r(i,j+1,k)+ε_r(i,j,k-1)+ε_r(i,j,k+1)}/7

図4-3に1つのデータの誘電率分布を示します。
Z面でスライスした図を順に示しています。 場所、大きさ、誘電率が異なる2個の直方体が存在することがわかります。

4.4 アンテナ位置の比較

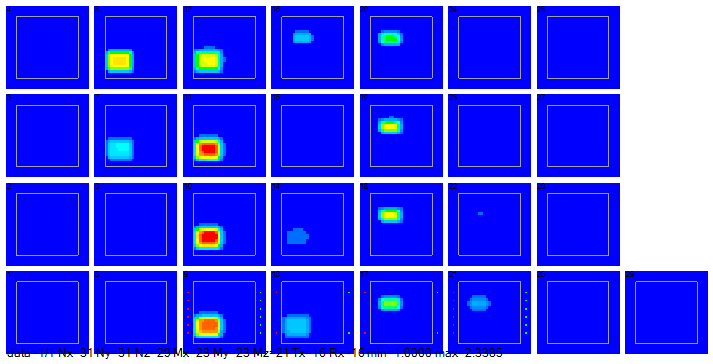
図4-1の4つのアンテナ位置の損失の収束状況を図4-4に示します。
case-1,case-2がほぼ同じで最良であり、case-3はやや劣り、case-4は非常に悪くなります。
これからアンテナ位置は面内を網羅することが大切であることがわかります。 図4-2からcase-4はS行列の変化が緩やかですが誘電率の推定には不向きです。
以下ではcase-2のみを考えます。

4.5 データ数についての考察

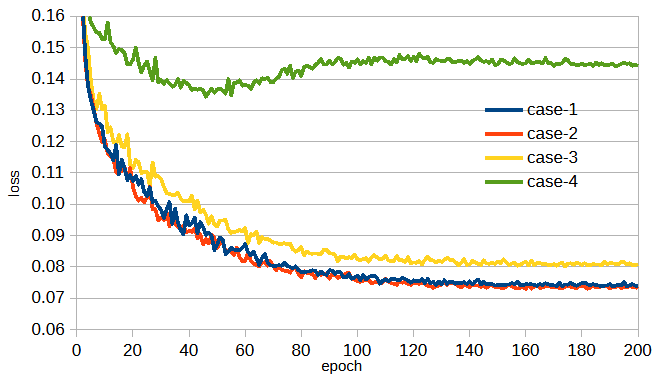
図4-5にデータ数を変えたときの収束状況を示します。
2次元モデルと同じく、 データ数が多いほど最終的な損失が小さいだけでなく収束も安定してかつ速いことがわかります。

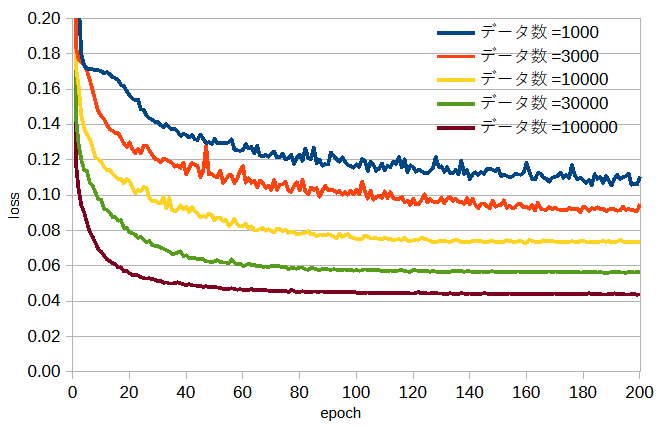
図4-6にデータ数を変えた時の損失の最小値（図4-5の最小値）を示します。
2次元モデルと同じく、 データ数が多いほど損失が小さくなることがわかります。

4.6 誘電率分布の推定結果

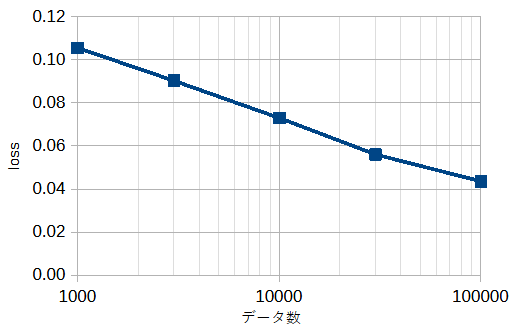
図4-7に3個のデータの誘電率分布の推定結果を示します。
Z面についてスライスした図であり、 左右で正解と推定値の2個1組のペアになっています。
いずれの場合も場所、形、誘電率が正しく推定できていることがわかります。

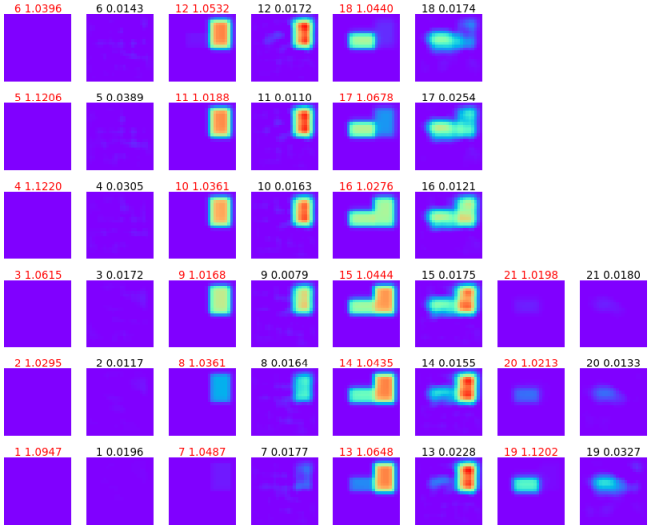
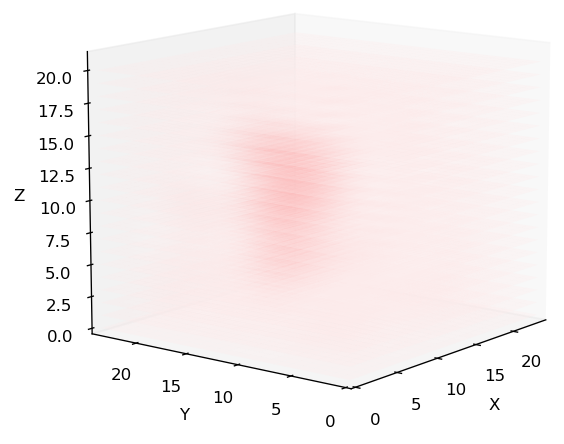
図4-8に誘電率分布の推定結果の3D表示を示します。
赤が濃いほど誘電率が大きいことを表します。
中央付近の誘電率が大きいことがわかりますが、 この図からは定量的なことはわかりません。