ファイル(fddl.zip) をダウンロードして、
適当なフォルダに展開してください。ファイル構成は以下の通りです。
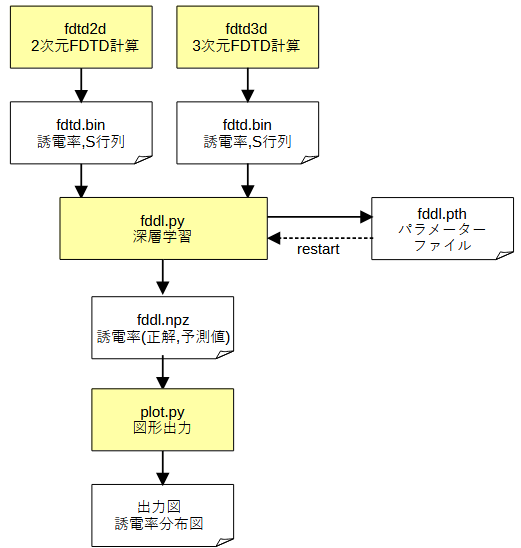
図5-1にシステム構成図を示します。

ファイルMain.cを編集して計算条件を設定してください。
リスト5-1 2次元版のデータ入力(Main.cの一部)
const int Ndata = 1000; // データ数
const int Nrect = 3; // 長方形数
const int Lrect[] = {3, 7, 1}; // 長方形パラメーター(最小,最大,余白)
const float Eps[] = {1.5f, 2.5f}; // 誘電率(最小,最大)
const float Sig[] = {0.02f, 0.08f}; // 導電率[S/m](最小,最大)
const int Nsmot = 2; // 平滑化回数(0以上)
const int NTx = 16; // 送信点数
const int NRx = 16; // 受信点数
const int DTx = 1; // 送信点間隔セル数
const int DRx = 1; // 受信点間隔セル数
const float Dx = 0.005f; // X方向セルサイズ
const float Dy = 0.005f; // Y方向セルサイズ
const int Nout = 4; // 外部領域セル数
const int Lant = 2; // アンテナ位置(対象領域境界からの距離)
const int ABC = 6; // PML層数(0のときはMur一次)
const float Freq = 3e9f; // 周波数
const int Niter = 600; // タイムステップ数
const float Eps0 = 1; // 背景媒質比誘電率
const float Sig0 = 0; // 背景媒質導電率[S/m]
リスト5-2 3次元版のデータ入力(Main.cの一部)
const int Ndata = 1000; // データ数
const int Nrect = 2; // 直方体数
const int Lrect[] = {3, 11, 1}; // 直方体パラメーター(最小,最大,余白)
const float Eps[] = {1.5f, 2.5f}; // 誘電率(最小,最大)
const float Sig[] = {0.02f, 0.08f}; // 導電率[S/m](最小,最大)
const int Nsmot = 2; // 平滑化回数(0以上)
const int NTx = 16; // 送信点数(16限定)
const int NRx = 16; // 受信点数(16限定)
const float Dx = 0.005f; // X方向セルサイズ
const float Dy = 0.005f; // Y方向セルサイズ
const float Dz = 0.005f; // Z方向セルサイズ
const int Nout = 4; // 外部領域セル数
const int Lant = 2; // アンテナ位置(対象領域境界からの距離)
const int ABC = 6; // PML層数(0のときはMur一次)
const float Freq = 3e9f; // 周波数
const int Niter = 300; // タイムステップ数
const float Eps0 = 1; // 背景媒質比誘電率
const float Sig0 = 0; // 背景媒質導電率[S/m]
FDTDプログラムをビルドするには、
2次元モデルはfdtd2dで3次元モデルはfdtd3dで以下のコマンドを実行してください。
いくつかのファイルはfdtd2dとfdtd3dで共通なので両者は同じ方法でビルドしてください。
計算速度は cl.exe < clang.exe < gcc です。
| ビルドコマンド | OS | コンパイラー | 実行プログラム |
|---|---|---|---|
| $ nmake.exe -f Makefile_cl | Windows | cl.exe | fdtd2d.exe または fdtd3d.exe |
| $ nmake.exe -f Makefile_cl_mpi | Windows | cl.exe | fdtd2d.exe または fdtd3d.exe (MPI対応) |
| $ nmake.exe -f Makefile_clang | Windows | clang.exe | fdtd2d.exe または fdtd3d.exe |
| $ nmake.exe -f Makefile_clang_mpi | Windows | clang.exe | fdtd2d.exe または fdtd3d.exe (MPI対応) |
| $ make -f Makefile_gcc | LinuxまたはWSL2 | gcc | fdtd2d または fdtd3d |
| $ make -f Makefile_gcc_mpi | LinuxまたはWSL2 | mpicc | fdtd2d または fdtd3d (MPI対応) |
FDTDプログラムはデータに関して独立した計算なので、
OpenMP(共有メモリー環境、スレッド並列)またはMPI(分散メモリー環境、プロセス並列)
で並列計算することができます。計算時間はスレッド数分の1、かつプロセス数分の1になります。
それぞれの環境で以下のコマンドを実行してください。
$ fdtd2d.exe 1スレッド, fdtd.bin出力 $ fdtd2d.exe 8 8スレッド, fdtd.bin出力 $ fdtd2d.exe 8 foo.bin 8スレッド, foo.bin出力 $ mpiexec.exe -n 2 fdtd2d.exe 4 foo.bin 2プロセス, 4スレッド, foo.bin出力(MPIでビルドしたとき)
$ fdtd3d.exe 1スレッド, fdtd.bin出力 $ fdtd3d.exe 8 8スレッド, fdtd.bin出力 $ fdtd3d.exe 8 foo.bin 8スレッド, foo.bin出力 $ mpiexec.exe -n 2 fdtd3d.exe 4 foo.bin 2プロセス, 4スレッド, foo.bin出力(MPIでビルドしたとき)
$ ./fdtd2d 1スレッド, fdtd.bin出力 $ ./fdtd2d 8 8スレッド, fdtd.bin出力 $ ./fdtd2d 8 foo.bin 8スレッド, foo.bin出力 $ mpiexec -n 2 fdtd2d 4 foo.bin 2プロセス, 4スレッド, foo.bin出力(MPIでビルドしたとき)
$ ./fdtd3d 1スレッド, fdtd.bin出力 $ ./fdtd3d 8 8スレッド, fdtd.bin出力 $ ./fdtd3d 8 foo.bin 8スレッド, foo.bin出力 $ mpiexec -n 2 fdtd3d 4 foo.bin 2プロセス, 4スレッド, foo.bin出力(MPIでビルドしたとき)
(注1)
MPI版は複数ノードで実行するときに使用し、その他の設定が必要ですが、ここでは説明は省略します。
通常は1ノードで非MPI版を使用してください。
(注2)
デバッグを行って図形出力するときは、
OpenFDTD等に付属している2次元図形表示プログラムev2d.exeを使用してください。
ファイルfddl.pyを編集して計算条件を設定してください。
リスト5-3 深層学習プログラムのデータ入力(fddl.pyの一部)
# FDTD計算結果ファイル名(誘電率とS行列からなる)
fdtd_bin = '../fdtd2d/fdtd.bin'
#fdtd_bin = '../fdtd3d/fdtd.bin'
# モデルファイル
modelfile = 'fddl.pth'
load_model = 0 # 通常0, 前回保存したmodelfileからrestartするとき1
save_model = 1 # 通常1, 計算終了時にmodelfileを保存しないとき0
# 計算パラメーター
ndata = 1000 # データ数, -1のときはすべてのデータ
batch_size = 50 # バッチサイズ, 通常50-100程度
num_epochs = 100 # エポック数
component = 1 # S行列成分, 1=S, 2=Re(S),Im(S), 3=Re(S),Im(S),S
train_ratio = 0.8 # 訓練データの割合(通常0.8程度, テストのときは0)
深層学習プログラムはPythonで記述されているのでビルド作業は不要です。
実行する前に、numpy, matplotlib, torch, torchvision をインストールしてください。
深層学習を行うには下記のコマンドを実行してください。
$ python fddl.py
計算結果を図形出力するには下記のコマンドを実行してください。
$ python plot.py
2次元FDTDの計算時間は以下のように評価されます。
2次元FDTDの計算時間 ∝ Nx * Ny * タイムステップ数 * Tx * データ数 / スレッド数 / プロセス数
計算時間の1例として以下のようになります。
・計算条件:Nx=Ny=17, Tx=16, タイムステップ数=600, データ数=100000
・ハードウェア: AMD Ryzen 7 7840HS, 8コア16スレッド
・計算時間: 477秒
3次元FDTDの計算時間は以下のように評価されます。
3次元FDTDの計算時間 ∝ Nx * Ny * Nz * タイムステップ数 * Tx * データ数 / スレッド数 / プロセス数
計算時間の1例として以下のようになります。
・計算条件:Nx=Ny=32, Nz=29, Tx=16, タイムステップ数=300, データ数=100000
・ハードウェア: FOCUSスパコン[5], Sシステム, AMD EPYC 9654, 96コア×2CPU×5ノード=960コア
・計算時間: 1262秒
深層学習の計算時間は以下のように評価されます。
深層学習の計算時間 ∝ エポック数 * データ数 * パラメータ数
計算時間の1例として以下のようになります。
・計算条件:エポック数=200, データ数=100000, パラメーター数=5,980,705(2D), 9,015,104(3D)
・ハードウェア: NVIDIA GeForce RTX 4060 Laptop, 3072コア
・計算時間: 3480秒(2D), 10660秒(3D)