SIMD(Single Instruction Multiple Data)とは複数のデータをベクトルレジスタに格納し一度の命令で複数の演算を行うものです。
IntelまたはAMDのCPU(x86/x64系)は標準でこの機能を持っています。
SSEやAVXを使用すると、理想的には表4-1の数値だけ速くなります。
| SIMDの種類 | ビット数 | 単精度(32ビット) | 倍精度(64ビット) |
|---|---|---|---|
| SSE | 128 | 4個 | 2個 |
| AVX | 256 | 8個 | 4個 |
| AVX-512 | 512 | 16個 | 8個 |
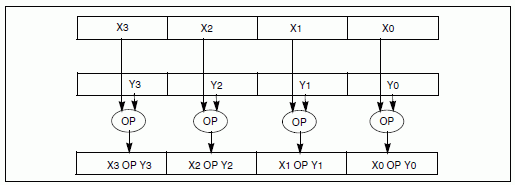
SIMD演算(SSEの場合)の代表例を図4-1に示します。
128ビットのベクトルレジスタに4個の単精度浮動小数点が入ります。
二つのベクトルレジスタ間の演算を一度に行い、結果がベクトルレジスタに入ります。

SIMD演算のプログラミングには、以下の二通りがあります。
(1)アセンブラを使用する。
(2)組み込み関数を使用する。
ここではコーディングのしやすさから(2)の方法を用います。
アセンブラの命令コードと組み込み関数がほぼ1対1に対応します。
両者の計算速度は同じです。
ヘッダーファイル
組み込み関数を使用するには関数が宣言されたヘッダーファイルをincludeする必要があります。
ヘッダーファイルはSIMDの初代のMMX(64ビット演算)の"mmintrin.h"から世代を重ね、現在は"immintrin.h"です。
ヘッダーファイルは旧世代の関数を含みますので、"#include <immintrin.h>"
と宣言するだけですべてのSSE/AVX関数を使用することができます。
組み込み関数
よく使う組み込み関数を表4-2に示します。
関数名はすべて"_mm"で始まります。AVXでは"_mm"が"_mm256"に変わります。
関数名の"_ps"の"p"は"Packed"を意味します。
これはレジスタの4個(AVXでは8個)すべての演算を行うことを意味します。
最下位のみの演算を行うときは"s"となります。
"_ps"の"s"は単精度(float)を意味します。倍精度(double)のときは"d"となります。
倍精度では128ビットレジスタに2個のデータが入ります(AVXでは256ビットに4個)。
レジスタの型はSSEでは"__m128"、AVXでは"__m256"です。
"_"は2個、"m"は1個であることに注意してください。
これ以外の関数については[1][2]を参考にしてください。
| 関数名 | 機能 | 対応する命令コードとその意味 |
|---|---|---|
| _mm_load_ps | メモリーからレジスタに移動する | MOVAPS Move Aligned Packed Single-Precision Floating-Point Values |
| _mm_store_ps | レジスタからメモリーに移動する | 同上 |
| _mm_add_ps | レジスタ同士の加算 | ADDPS Add Packed Single-Precision Floating-Point Values |
| _mm_sub_ps | レジスタ同士の減算 | SUBPS Subtract Packed Single-Precision Floating-Point Values |
| _mm_mul_ps | レジスタ同士の乗算 | MULPS Multiply Packed Single-Precision Floating-Point Values |
リスト4-1にベクトル和とベクトルの内積をSIMDを用いて計算するプログラムを示します。
リスト4-1 SIMDプログラム(simd.c)
1 /*
2 simd.c (SIMD)
3
4 VC++ : cl.exe /O2 simd.c
5 gcc : gcc -O2 -mavx simd.c -o simd
6
7 Usage:
8 > simd <1|2> <num> <loop> [sse|avx]
9 */
10
11 #include <stdlib.h>
12 #include <stdio.h>
13 #include <string.h>
14 #include <time.h>
15 #include <immintrin.h>
16
17 static void vadd(int simd, int n, const float a[], const float b[], float c[])
18 {
19 int ne = 0;
20
21 if (simd == 1) {
22 // SSE
23 ne = (n / 4) * 4;
24 for (int i = 0; i < ne; i += 4) {
25 _mm_storeu_ps(c + i,
26 _mm_add_ps(
27 _mm_loadu_ps(a + i),
28 _mm_loadu_ps(b + i)));
29 }
30 }
31 else if (simd == 2) {
32 // AVX
33 ne = (n / 8) * 8;
34 for (int i = 0; i < ne; i += 8) {
35 _mm256_storeu_ps(c + i,
36 _mm256_add_ps(
37 _mm256_loadu_ps(a + i),
38 _mm256_loadu_ps(b + i)));
39 }
40 }
41
42 for (int i = ne; i < n; i++) {
43 c[i] = a[i] + b[i];
44 }
45 }
46
47 static float sdot(int simd, int n, const float a[], const float b[])
48 {
49 int ne = 0;
50 float sum = 0;
51
52 if (simd == 1) {
53 // SSE
54 float fsum[4];
55 __m128 vsum;
56 ne = (n / 4) * 4;
57 vsum = _mm_setzero_ps();
58 for (int i = 0; i < ne; i += 4) {
59 vsum = _mm_add_ps(vsum,
60 _mm_mul_ps(_mm_loadu_ps(a + i),
61 _mm_loadu_ps(b + i)));
62 }
63 _mm_storeu_ps(fsum, vsum);
64 sum = fsum[0] + fsum[1] + fsum[2] + fsum[3];
65 }
66 else if (simd == 2) {
67 // AVX
68 float fsum[8];
69 __m256 vsum;
70 ne = (n / 8) * 8;
71 vsum = _mm256_setzero_ps();
72 for (int i = 0; i < ne; i += 8) {
73 vsum = _mm256_add_ps(vsum,
74 _mm256_mul_ps(_mm256_loadu_ps(a + i),
75 _mm256_loadu_ps(b + i)));
76 }
77 _mm256_storeu_ps(fsum, vsum);
78 sum = fsum[0] + fsum[1] + fsum[2] + fsum[3]
79 + fsum[4] + fsum[5] + fsum[6] + fsum[7];
80 }
81
82 for (int i = ne; i < n; i++) {
83 sum += a[i] * b[i];
84 }
85
86 return sum;
87 }
88
89 int main(int argc, char **argv)
90 {
91 int calc = 1;
92 int simd = 0;
93 int n = 1000;
94 int nloop = 1000;
95 float *a = NULL, *b = NULL, *c = NULL;
96 char *str[3] = {"none", "SSE", "AVX"};
97
98 // arguments
99 if (argc >= 4) {
100 calc = atoi(argv[1]);
101 n = atoi(argv[2]);
102 nloop = atoi(argv[3]);
103 }
104 if (argc >= 5) {
105 if (!strcmp(argv[4], "sse")) {
106 simd = 1;
107 }
108 else if (!strcmp(argv[4], "avx")) {
109 simd = 2;
110 }
111 }
112
113 // alloc
114 size_t size = n * sizeof(float);
115 if (calc == 1) {
116 a = (float *)malloc(size);
117 b = (float *)malloc(size);
118 c = (float *)malloc(size);
119 }
120 else if (calc == 2) {
121 a = (float *)malloc(size);
122 b = (float *)malloc(size);
123 }
124
125 // setup problem
126 for (int i = 0; i < n; i++) {
127 a[i] = i + 1.0f;
128 b[i] = i + 1.0f;
129 }
130
131 // timer
132 clock_t t0 = clock();
133
134 // calculation
135 double result = 0, exact = 0;
136 if (calc == 1) {
137 // vadd
138 for (int loop = 0; loop < nloop; loop++) {
139 vadd(simd, n, a, b, c);
140 }
141 result = 0;
142 for (int i = 0; i < n; i++) {
143 result += c[i];
144 }
145 exact = (double)n * (n + 1);
146 }
147 else if (calc == 2) {
148 // sdot
149 double sum = 0;
150 for (int loop = 0; loop < nloop; loop++) {
151 sum += sdot(simd, n, a, b);
152 }
153 result = sum / nloop;
154 exact = (double)n * (n + 1) * (2 * n + 1) / 6.0;
155 }
156
157 // timer
158 clock_t t1 = clock();
159 double cpu = (double)(t1 - t0) / CLOCKS_PER_SEC;
160
161 // output
162 printf("%d N=%d L=%d %.6e(%.6e) err=%.1e %.3f[sec] %s\n",
163 calc, n, nloop, result, exact, fabs(result - exact) / exact, cpu, str[simd]);
164
165 // free
166 if (calc == 1) {
167 free(a);
168 free(b);
169 free(c);
170 }
171 else if (calc == 2) {
172 free(a);
173 free(b);
174 }
175
176 return 0;
177 }
配列とアラインメント
ここでは配列の確保/解放に通常のmalloc/free関数を使用しています。
Intelのドキュメント[1]にはアラインメントを行うように書かれていますが、
現在の環境では速度に影響がないので、
コードを簡単にするためにアラインメントを行っていません。
ここでアラインメントとはアドレスが16バイト(AVXでは32バイト)の倍数になるように、
コンパイラに指示することを意味します。
アラインメントを行うには以下のように書き変えます。
a = (float *)malloc(size); → a = (float *)_mm_malloc(size, 16);
free(a); → _mm_free(a);
このとき同時に、ベクトルレジスタを主メモリーにコピーする配列も以下のように宣言します。
float fsum[4]; → __declspec(align(16)) float fsum[4]; (VC++の場合)
float fsum[4]; → __attribute__((aligned(16))) float fsum[4]; (gccの場合)
ここで、AVXのときは16は32に、4は8になります。
さらに、loadu/storeu関数はload/store関数になります。
"u"はアラインメントされていないことを表します。
ループ長が4または8の倍数でないとき
通常のアプリケーションではループ長に制限はなく、4または8の倍数とは限りません。
このようなときは、24,34,58,72行目のように4または8の倍数までをSIMDで計算し、
残りを42-44,82-84行目のようにSIMDを使わずに計算します。
SIMDがないときは"ne=0"なので残りはループ全体を表します。
以上の方法を用いるとSIMDコードと非SIMDコードを共存させることができます。
なお、20行目では和をとる変数をfloatとしていますが精度上はdoubleが望ましいです。
計算時間もほとんど変わりません。
コンパイル・リンク方法
VC++ではコンパイル・リンクオプションは特に必要ありません。
> cl.exe /O2 simd.c
gccではSSEを使うにはコンパイル・リンクオプションは特に必要ありませんが、
AVXを使うにはコンパイルオプションに"-mavx"が必要です。
> gcc -O2 -mavx simd.c -o simd
自動ベクトル化
VC++ではコンパイルオプション"/Qvec-report:1"をつけると、
自動ベクトル化されたループが表示されます。
(表示されていないループは自動ベクトル化されていません)
下記のメッセージから、ベクトル和(42行目)は自動ベクトル化され、
ベクトル内積(82行目)は自動ベクトル化されないことがわかります。
従ってベクトル内積はSIMDを使用しないと計算時間がかかることが予想されます。
$ cl.exe /c /O2 /Qvec-report:1 /nologo simd.c simd.c --- 分析関数: vadd simd.c(42) : info C5001: ループがベクトル化されています --- 分析関数: main simd.c(126) : info C5001: ループがベクトル化されています
プログラムの実行方法
プログラムの実行方法は以下の通りです。
> simd 1|2 配列の大きさ 繰り返し回数 [sse|avx]
例えば以下のようになります。
> simd 1 1000000 1000 sse
最初の引数が1のときベクトル和、2のときベクトル内積を計算します。
最後の引数(sseまたはavx)がないときはSIMDを使用しません。
繰り返し回数は計算時間の測定誤差を小さくするためです。
表4-3にベクトル和の計算時間を示します。
SIMDを使わないときとSSEまたはAVXを使ったときの結果です。
配列の大きさ(=N)と繰り返し回数(=L)の積は一定(=1010)です。
従って全体の演算量は同じです。
使用メモリーは12Nバイトです。
従って表の下になるほど使用メモリーが小さくなりキャッシュに乗りやすくなります。
No.3-4のSIMDなしのときに限りVC++とGCCの計算時間が異なります。
このときVC++は自動ベクトル化され、SIMDありとほぼ同じ計算時間になりますが、
GCCは自動ベクトル化されないために、SIMDありと比べて計算時間が大幅に増えます。
No.1-2は使用メモリーがキャッシュに乗らないために、
SIMDの有無で計算時間が変わりません。
以上から、ベクトル和の計算では、自動ベクトル化できないコンパイラのときに限り、
SIMDプログラムが意味を持ちます。
| No. | 配列の大きさN | 繰り返し回数L | VC++ | GCC | ||||
|---|---|---|---|---|---|---|---|---|
| SIMDなし | SSE | AVX | SIMDなし | SSE | AVX | |||
| 1 | 10,000,000 | 1,000 | 5.54秒(1.0) | 5.62秒(0.99) | 5.70秒(0.97) | 6.31秒(1.0) | 5.62秒(1.12) | 5.70秒(1.11) |
| 2 | 1,000,000 | 10,000 | 5.94秒(1.0) | 6.19秒(0.96) | 5.87秒(1.01) | 6.54秒(1.0) | 5.71秒(1.15) | 5.81秒(1.13) |
| 3 | 100,000 | 100,000 | 1.14秒(1.0) | 1.15秒(0.99) | 1.06秒(1.08) | 4.73秒(1.0) | 1.13秒(4.19) | 1.19秒(3.97) |
| 4 | 10,000 | 1,000,000 | 0.91秒(1.0) | 0.91秒(1.00) | 0.90秒(1.01) | 4.74秒(1.0) | 0.89秒(5.33) | 0.90秒(5.27) |
表4-4にベクトル内積の計算時間を示します。
SIMDを使わないときとSSEまたはAVXを使ったときの結果です。
配列の大きさ(=N)と繰り返し回数(=L)の積は一定(=1010)です。
従って全体の演算量は同じです。
使用メモリーは8Nバイトです。
従って表の下になるほど使用メモリーが小さくなりキャッシュに乗りやすくなります。
SIMDを使わないときはNo.1-4及びVC++/GCCで計算時間はほぼ一定です。
SIMDを使うときはVC++/GCCともに、No.3-4ではSSEで4倍、AVXで8倍と理想的な速さになります。
ベクトル内積の計算はreduction演算なので、VC++/GCCともに自動ベクトル化ができず、
SIMDプログラムで高速化が期待できます。
ただし、ここでは評価していませんが、
Intelのコンパイラ[23]を用いるとかなり複雑なアルゴリズムも自動ベクトル化できる可能性があります。
| No. | 配列の大きさN | 繰り返し回数L | VC++ | GCC | ||||
|---|---|---|---|---|---|---|---|---|
| SIMDなし | SSE | AVX | SIMDなし | SSE | AVX | |||
| 1 | 10,000,000 | 1,000 | 7.17秒(1.0) | 3.05秒(2.35) | 2.75秒(2.61) | 7.27秒(1.0) | 3.01秒(2.42) | 2.75秒(2.64) |
| 2 | 1,000,000 | 10,000 | 7.52秒(1.0) | 3.10秒(2.43) | 2.73秒(2.75) | 7.27秒(1.0) | 2.61秒(2.79) | 2.34秒(3.11) |
| 3 | 100,000 | 100,000 | 7.03秒(1.0) | 1.78秒(3.95) | 0.89秒(7.90) | 7.07秒(1.0) | 1.78秒(3.97) | 0.90秒(7.86) |
| 4 | 10,000 | 1,000,000 | 7.00秒(1.0) | 1.76秒(3.98) | 0.88秒(7.95) | 7.04秒(1.0) | 1.76秒(4.00) | 0.88秒(8.00) |