OpenMP[3][4]とは、共有メモリー環境で並列計算を行うプログラミング技術であり、
複数のコアを持ったCPUで、
同時に複数のスレッドを実行して処理を分割し計算時間を短縮するものです。
1台のコンピュータに複数のCPUが搭載されていればさらにその個数だけ速くなります。
OpenMPは次節で述べるマルチスレッドの一種ですが、
プログラミング方法が異なるので、ここでは特に"OpenMP"と呼びます。
OpenMPでは並列処理を行うfor文のすぐ上に"#pragma omp"で始まる指示文(ディレクティブ)を挿入し、
コンパイルオプションでOpenMPを使用していることを知らせます。
コンパイルオプションがないときは指示文はコメントとみなされ
1コアのみを使用する逐次プログラムができます。
OpenMPは元のソースコードに一切手を加えることなく並列化できますので、
OpenMPで並列化できるアルゴリズムのときは最も簡単にプログラミングできます。
また、並列化したい場所だけを順々に並列化できますのでプログラミングの生産性が高くなります。
OpenMPはOSやコンパイラーに依存しない規格なので、
同じソースコードがさまざまな環境で動きます。
リスト5-1にベクトル和またはベクトル内積をOpenMPで並列計算するプログラムを示します。
"SIMD"の章で説明したようにベクトル内積はSIMDを用いると高速化されるのでSIMDを使用した関数(sdot_simd)も実装しています。
リスト5-1 OpenMPプログラム(omp.c)
1 /*
2 omp.c (OpenMP)
3
4 VC++ : cl.exe /O2 /openmp omp.c
5 gcc : gcc -O2 -fopenmp omp.c -o omp
6
7 Usage :
8 > omp {1|2} <num> <loop> <thread> [sse|avx]
9 */
10
11 #include <stdlib.h>
12 #include <stdio.h>
13 #include <string.h>
14 #include <time.h>
15 #include <immintrin.h>
16
17 #ifdef _OPENMP
18 #include <omp.h>
19 #endif
20
21 #ifndef _WIN32
22 #include <sys/time.h>
23 #endif
24
25 static inline void vadd(int n, const float a[], const float b[], float c[])
26 {
27 int i;
28 #ifdef _OPENMP
29 #pragma omp parallel for //schedule(static, 1)
30 #endif
31 for (i = 0; i < n; i++) {
32 c[i] = a[i] + b[i];
33 }
34 }
35
36 static inline double sdot(int n, const float a[], const float b[])
37 {
38 double sum = 0;
39 int i;
40 #ifdef _OPENMP
41 #pragma omp parallel for reduction(+:sum)
42 #endif
43 for (i = 0; i < n; i++) {
44 sum += a[i] * b[i];
45 }
46
47 return sum;
48 }
49
50 static inline double sdot_simd(int n, const float a[], const float b[], int nthread, int simd)
51 {
52 double *sum_thread = (double *)malloc(nthread * sizeof(double));
53 memset(sum_thread, 0, nthread * sizeof(double));
54
55 #ifdef _OPENMP
56 #pragma omp parallel
57 #endif
58 {
59 int ithread = 0;
60 #ifdef _OPENMP
61 ithread = omp_get_thread_num();
62 #endif
63 const int lsimd = 4 * simd; // = 4/8
64 const int lthread = (n + (nthread - 1)) / nthread;
65 const int ns = ithread * lthread;
66 const int ne = ((ns + lthread) > n) ? n : (ns + lthread);
67 const int nc = ns + ((ne - ns) / lsimd) * lsimd;
68
69 if (simd == 1) {
70 // SSE
71 float fsum[4];
72 __m128 vsum = _mm_setzero_ps();
73 for (int i = ns; i < nc; i += lsimd) {
74 vsum = _mm_add_ps(vsum,
75 _mm_mul_ps(_mm_loadu_ps(a + i),
76 _mm_loadu_ps(b + i)));
77 }
78 _mm_storeu_ps(fsum, vsum);
79 sum_thread[ithread] = fsum[0] + fsum[1] + fsum[2] + fsum[3];
80 }
81 else if (simd == 2) {
82 // AVX
83 float fsum[8];
84 __m256 vsum = _mm256_setzero_ps();
85 for (int i = ns; i < nc; i += lsimd) {
86 vsum = _mm256_add_ps(vsum,
87 _mm256_mul_ps(_mm256_loadu_ps(a + i),
88 _mm256_loadu_ps(b + i)));
89 }
90 _mm256_storeu_ps(fsum, vsum);
91 sum_thread[ithread] = fsum[0] + fsum[1] + fsum[2] + fsum[3]
92 + fsum[4] + fsum[5] + fsum[6] + fsum[7];
93 }
94
95 for (int i = nc; i < ne; i++) {
96 sum_thread[ithread] += a[i] * b[i];
97 }
98 }
99
100 double sum = 0;
101 for (int ithread = 0; ithread < nthread; ithread++) {
102 sum += sum_thread[ithread];
103 }
104
105 return sum;
106 }
107
108 int main(int argc, char **argv)
109 {
110 int calc = 1;
111 int nthread = 1;
112 int n = 1000;
113 int nloop = 1000;
114 int simd = 0;
115 float *a = NULL, *b = NULL, *c = NULL;
116 #ifdef _WIN32
117 clock_t t0, t1;
118 #else
119 struct timeval t0, t1;
120 #endif
121
122 // arguments
123 if (argc >= 5) {
124 calc = atoi(argv[1]);
125 n = atoi(argv[2]);
126 nloop = atoi(argv[3]);
127 nthread = atoi(argv[4]);
128 }
129 if (argc >= 6) {
130 if (!strcmp(argv[5], "sse")) {
131 simd = 1;
132 }
133 else if (!strcmp(argv[5], "avx")) {
134 simd = 2;
135 }
136 }
137
138 #ifdef _OPENMP
139 // threads
140 omp_set_num_threads(nthread);
141 #endif
142
143 // alloc
144 size_t size = n * sizeof(float);
145 if (calc == 1) {
146 a = (float *)malloc(size);
147 b = (float *)malloc(size);
148 c = (float *)malloc(size);
149 }
150 else if (calc == 2) {
151 a = (float *)malloc(size);
152 b = (float *)malloc(size);
153 }
154
155 // setup problem
156 for (int i = 0; i < n; i++) {
157 a[i] = i + 1.0f;
158 b[i] = i + 1.0f;
159 }
160
161 // timer
162 #ifdef _WIN32
163 t0 = clock();
164 #else
165 gettimeofday(&t0, NULL);
166 #endif
167
168 // calculation
169 double sum = 0;
170 if (calc == 1) {
171 // add vector
172 for (int loop = 0; loop < nloop; loop++) {
173 vadd(n, a, b, c);
174 }
175 for (int i = 0; i < n; i++) {
176 sum += c[i];
177 }
178 }
179 else if (calc == 2) {
180 // dot product
181 for (int loop = 0; loop < nloop; loop++) {
182 if (!simd) {
183 sum += sdot(n, a, b);
184 }
185 else {
186 sum += sdot_simd(n, a, b, nthread, simd);
187 }
188 }
189 sum /= nloop;
190 }
191
192 // timer
193 double cpu = 0;
194 #ifdef _WIN32
195 t1 = clock();
196 cpu = (double)(t1 - t0) / CLOCKS_PER_SEC;
197 #else
198 gettimeofday(&t1, NULL);
199 cpu = (t1.tv_sec - t0.tv_sec) + 1e-6 * (t1.tv_usec - t0.tv_usec);
200 #endif
201
202 // output
203 double exact = (calc == 1)
204 ? (double)n * (n + 1)
205 : (double)n * (n + 1) * (2 * n + 1) / 6.0;
206 printf("%d N=%d L=%d thread=%d %.6e(%.6e) err=%.1e %.3f[sec]\n",
207 calc, n, nloop, nthread, sum, exact, fabs(sum - exact) / exact, cpu);
208
209 // free
210 if (calc == 1) {
211 free(a);
212 free(b);
213 free(c);
214 }
215 else if (calc == 2) {
216 free(a);
217 free(b);
218 }
219
220 return 0;
221 }
OpenMP指示文
コンパイルオプション/openmpをつけるとマクロ"_OPENMP"が有効になります。
29行目と41行目でfor文を並列計算することを指示しています。
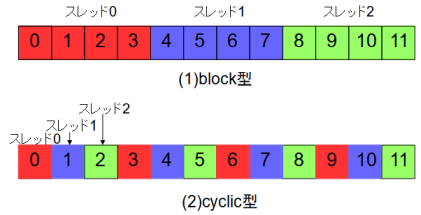
forループをスレッドで分割する方法には図5-1の2通りがあります。
それらを制御するにはschedule指示節を使用します。
schedule指示節がないときはblock型になります。
#pragma omp parallel for schedule(static) (block型)
#pragma omp parallel for schedule(static, 1) (cyclic型)
#pragma omp parallel for (block型)

reduction指示節
41行目ではベクトルの内積を並列計算するには、
すべてのスレッドが総和変数にアクセスするので以下のreduction指示節が必要になります。
reduction (operator:list)
ここで operator は加算("+")、乗算("*")などを表し、
list はreduction演算される変数名を表します。
OpenMP関数
140行目の omp_set_num_threads 関数で使用するスレッド数を指定します。
本関数を呼ばないときはスレッド数は論理コア数になります。
61行目の omp_get_thread_num 関数で並列領域のスレッド番号(=0,1,2,...)を取得します。
OpenMP関数を使用するには18行目の "#include <omp.h>" 文が必要です。
OpenMP関数の使用頻度は高くありませんが、詳しくは[3][4]を参考にしてください。
OpenMP並列領域
56行目のように "#pragma omp parallel" を指示したときは、
その下の{}で囲まれた部分が並列領域になります。
この中でスレッド番号に応じた処理を記述します。
本プログラムでは各並列領域でスレッド毎の部分和を計算し、
最後に100-103行で全スレッドの部分和を加えて全体の和を求めています。
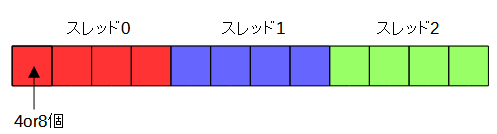
各スレッド内では図5-2のように4個(SSE)または8個(AVX)の単位で分割しSIMD演算を行います。
これは図5-1のblock型に相当します。
計算時間の計測
gccではclock関数は全スレッドの和になるので、
リスト5-1では計算時間を計測するためにgettimeofday関数を使用しています。
コンパイル・リンク方法
VC++ではコンパイルオプションに"/openmp"が必要です。
> cl.exe /O2 /openmp omp.c
gccではコンパイルオプションとリンクオプションに"-fopenmp"が必要です。
> gcc -O2 -fopenmp omp.c -o omp
プログラムの実行方法
プログラムの実行方法は以下の通りです。
> omp {1|2} 配列の大きさ 繰り返し回数 スレッド数 [sse|avx]
例えば以下のようになります。
> omp 1 1000000 1000 4 (ベクトル和を計算するとき)
> omp 2 1000000 1000 4 (ベクトル内積を計算するとき)
> omp 2 1000000 1000 4 avx (ベクトル内積をAVXで計算するとき)
繰り返し回数は計算時間の測定誤差を小さくするためです。
[sse|avx]はベクトル内積のときのみ有効です。
なお、OpenMP対応プログラムの実行にはvcomp140.dllファイルが必要です。
(Microsoft Visual Studio 2022の場合)
表5-1と図5-3にベクトル和の計算時間を示します。
SIMDは使用していません。
表5-1はblock型、図5-3はblock型とcyclic型です。
配列の大きさ(=N)と繰り返し回数(=L)の積は一定(=1010)です。従って全体の演算量は同じです。
使用メモリーは12Nバイトです。
従って、表の下になるほど使用メモリーが小さくなりキャッシュに乗りやすくなります。
スレッド数が少ないときは、No.3-4はキャッシュに入り、
自動ベクトル化の効果により計算時間が短くなります。
スレッド数が多いときは、No.2とNo.3のみOpenMP並列化の効果があり計算時間が短くなります。
図5-3の右の図からわかるようにcyclic型はスレッド数が増えるとむしろ計算時間が増え、
自動ベクトル化も無効になっています。
以上から、本ケースではblock型が優れていますが、
ループ内の演算量が多いときや一定でないときは結果が変わる可能性があります。
| No. | 配列の大きさN | 繰り返し回数L | 1スレッド | 2スレッド | 4スレッド | 8スレッド | 16スレッド |
|---|---|---|---|---|---|---|---|
| 1 | 10,000,000 | 1,000 | 5.53秒(1.0) | 4.70秒(1.18) | 4.78秒(1.16) | 4.81秒(1.15) | 5.34秒(1.04) |
| 2 | 1,000,000 | 10,000 | 5.93秒(1.0) | 4.79秒(1.24) | 3.59秒(1.65) | 0.98秒(6.05) | 1.16秒(5.11) |
| 3 | 100,000 | 100,000 | 1.13秒(1.0) | 0.57秒(1.98) | 0.27秒(4.19) | 0.21秒(5.38) | 0.24秒(4.71) |
| 4 | 10,000 | 1,000,000 | 0.94秒(1.0) | 0.73秒(1.29) | 0.83秒(1.13) | 0.84秒(1.12) | 1.14秒(0.82) |
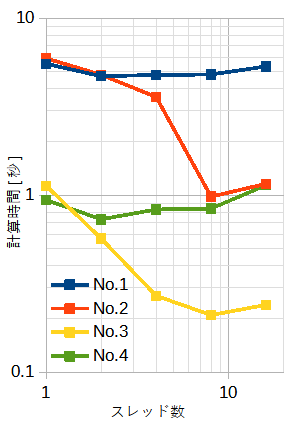
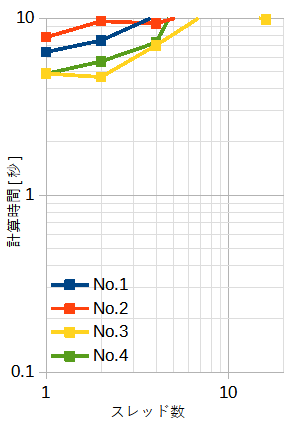
表5-2~表5-4にベクトル内積の計算時間を示します。
それぞれ、SIMDなし、SSE、AVXです。
ループ分割はblock型です。
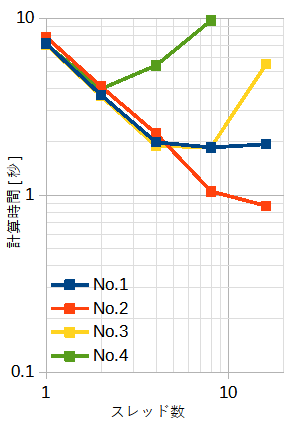
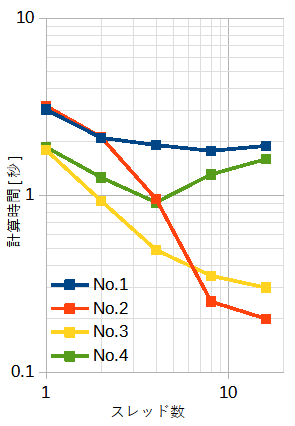
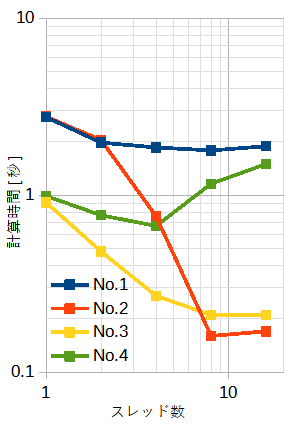
図5-4にそれぞれの計算時間を示します。
配列の大きさ(=N)と繰り返し回数(=L)の積は一定(=1010)です。従って全体の演算量は同じです。
使用メモリーは8Nバイトです。
従って、表の下になるほど使用メモリーが小さくなりキャッシュに乗りやすくなります。
スレッド数とSIMDの効果が複雑な特性を示します。
ベクトル内積では一般にSIMDの効果があり、さらにスレッド数を増やすとある程度速くなります。
| No. | 配列の大きさN | 繰り返し回数L | 1スレッド | 2スレッド | 4スレッド | 8スレッド | 16スレッド |
|---|---|---|---|---|---|---|---|
| 1 | 10,000,000 | 1,000 | 7.18秒(1.0) | 3.68秒(1.95) | 1.99秒(3.61) | 1.86秒(3.86) | 1.94秒(3.70) |
| 2 | 1,000,000 | 10,000 | 7.85秒(1.0) | 4.11秒(1.91) | 2.23秒(3.52) | 1.05秒(7.48) | 0.87秒(9.02) |
| 3 | 100,000 | 100,000 | 7.09秒(1.0) | 3.63秒(1.95) | 1.89秒(3.75) | 1.87秒(3.79) | 5.51秒(1.29) |
| 4 | 10,000 | 1,000,000 | 7.12秒(1.0) | 3.98秒(1.79) | 5.41秒(1.32) | 9.72秒(0.73) | 65.74秒(0.11) |
| No. | 配列の大きさN | 繰り返し回数L | 1スレッド | 2スレッド | 4スレッド | 8スレッド | 16スレッド |
|---|---|---|---|---|---|---|---|
| 1 | 10,000,000 | 1,000 | 3.04秒(1.0) | 2.11秒(1.44) | 1.92秒(1.58) | 1.78秒(1.71) | 1.90秒(1.60) |
| 2 | 1,000,000 | 10,000 | 3.19秒(1.0) | 2.13秒(2.42) | 0.95秒(1.96) | 0.25秒(12.76) | 0.20秒(15.95) |
| 3 | 100,000 | 100,000 | 1.80秒(1.0) | 0.93秒(1.94) | 0.49秒(3.67) | 0.35秒(5.14) | 0.30秒(6.00) |
| 4 | 10,000 | 1,000,000 | 1.87秒(1.0) | 1.26秒(1.48) | 0.91秒(2.05) | 1.31秒(1.43) | 1.60秒(1.17) |
| No. | 配列の大きさN | 繰り返し回数L | 1スレッド | 2スレッド | 4スレッド | 8スレッド | 16スレッド |
|---|---|---|---|---|---|---|---|
| 1 | 10,000,000 | 1,000 | 2.76秒(1.0) | 1.98秒(1.39) | 1.86秒(1.48) | 1.79秒(1.54) | 1.89秒(1.46) |
| 2 | 1,000,000 | 10,000 | 2.78秒(1.0) | 2.05秒(1.36) | 0.76秒(3.66) | 0.16秒(17.38) | 0.17秒(16.35) |
| 3 | 100,000 | 100,000 | 0.91秒(1.0) | 0.48秒(1.90) | 0.27秒(3.37) | 0.21秒(4.33) | 0.21秒(4.33) |
| 4 | 10,000 | 1,000,000 | 0.99秒(1.0) | 0.77秒(1.29) | 0.67秒(1.48) | 1.16秒(0.85) | 1.50秒(0.66) |