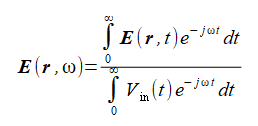 (2-10-1)
(2-10-1)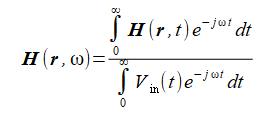 (2-10-2)
(2-10-2)
以上の方法で計算された時間領域の電磁界を指定した周波数でFourier変換することによって解析領域内の電磁界の調和界(=近傍電磁界、複素数)が得られます。
給電点モデルでは給電電圧のFourier変換で正規化します。給電点が複数あるときは第一給電点の電圧とします。
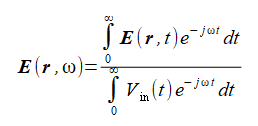 (2-10-1)
(2-10-1)
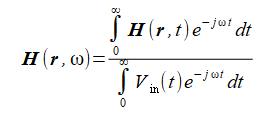 (2-10-2)
(2-10-2)
平面波入射モデルでは入射電磁界のFourier変換で正規化します。
ここでrcは計算領域の中心点です。
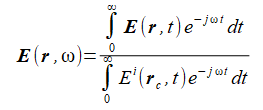 (2-10-3)
(2-10-3)
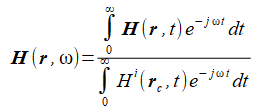 (2-10-4)
(2-10-4)
電流密度は式(2-1-1)の第一式から以下のようになります。
これは導体の上では導電流、誘電体の中では変位電流を意味します。
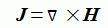 (2-10-5)
(2-10-5)
式(2-10-5)より電流のXYZ成分は以下のようになります。
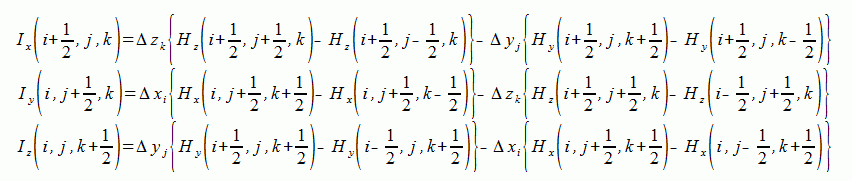 (2-10-6)
(2-10-6)
調和電界の各成分を振幅と位相で表現すると以下のようになります。
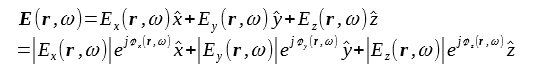 (2-10-7)
(2-10-7)
電界の各成分とその合成の時間波形は次式で計算されます。磁界についても同様です。
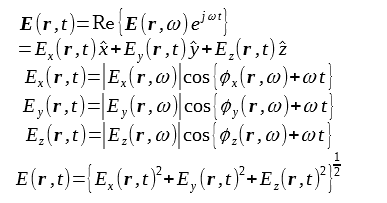 (2-10-8)
(2-10-8)