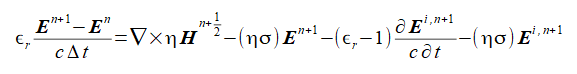 (2-3-1)
(2-3-1)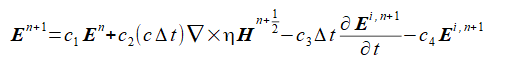 (2-3-2)
(2-3-2)
式(2-1-4)は式(2-1-6)において入射電磁界
(Ei,Hi)
をゼロとした式なので、ここではより一般的な式(2-1-6)の離散化を考えます。
FDTD法では基本式(2-1-6)を時間領域と空間領域で離散化します。
時間領域では磁界と電界を半時間幅ごとに交互にとります。
時間に関するインデックスをnとし、時間幅をΔtとします。
式(2-1-6)の第1式を時刻(n+1/2)Δtで離散化すると式(2-3-1)となり、
これから電界の最新項を求めると式(2-3-2)となります。
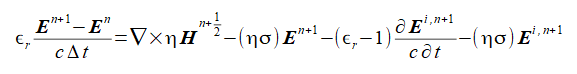 (2-3-1)
(2-3-1)
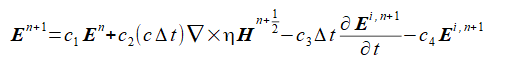 (2-3-2)
(2-3-2)
式(2-1-6)の第2式を時刻nΔtで離散化すると式(2-3-3)となり、
これから磁界の最新項を求めると式(2-3-4)となります。
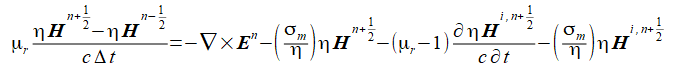 (2-3-3)
(2-3-3)
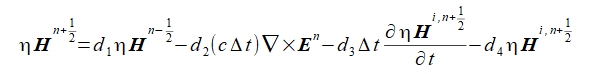 (2-3-4)
(2-3-4)
ここで係数c1,...,c4,d1,...,d4
は式(2-3-5)(2-3-6)で定義される無次元量の場所の関数です。
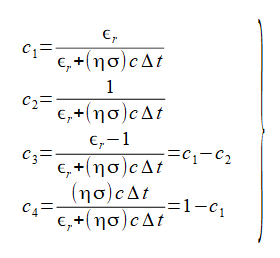 (2-3-5)
(2-3-5)
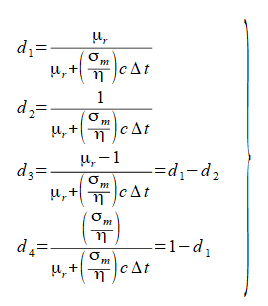 (2-3-6)
(2-3-6)
式(2-3-2)のXYZ成分は式(2-3-7)-(2-3-9)のようになります。
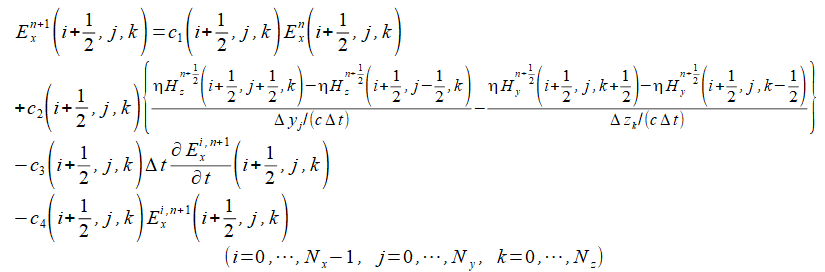 (2-3-7)
(2-3-7)
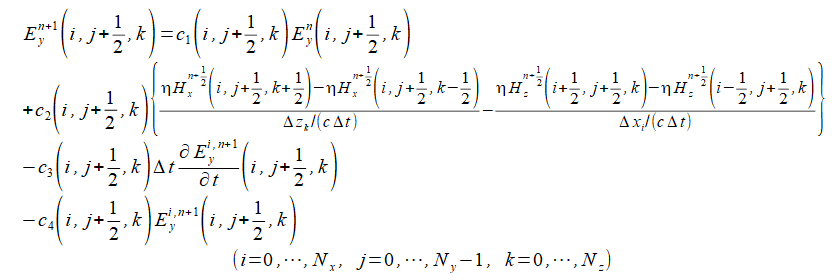 (2-3-8)
(2-3-8)
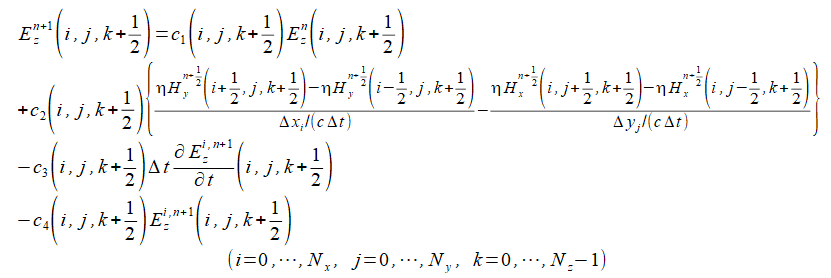 (2-3-9)
(2-3-9)
式(2-3-4)のXYZ成分は式(2-3-10)-(2-3-12)のようになります。
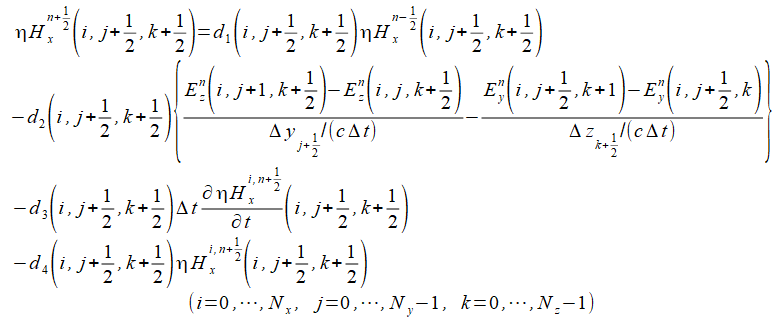 (2-3-10)
(2-3-10)
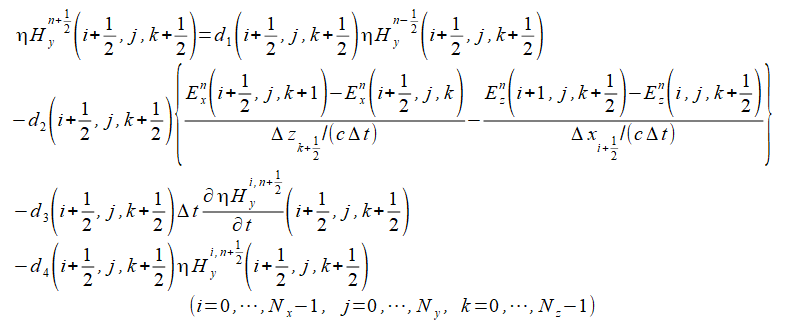 (2-3-11)
(2-3-11)
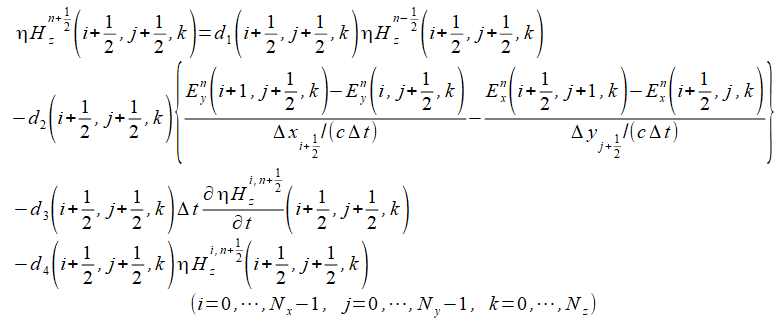 (2-3-12)
(2-3-12)
基本式が(2-1-4)のときは式(2-3-7)-(2-3-12)の右辺の第3項と第4項がなくなります。
反復計算が発散せずに安定に行われるためには、
時間幅について以下のCourant条件が必要です。
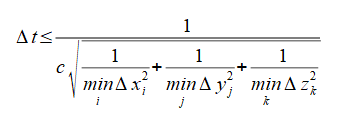 (2-3-13)
(2-3-13)