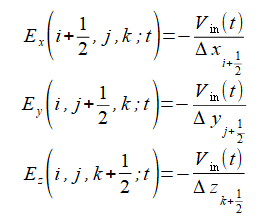(2-4-1)波源モデルとしては、給電点モデルと平面波入射モデルの2通りを考えます。
給電点モデルでは計算領域の内部に1個以上の給電点を置きます。
給電電圧の方向がX/Y/Z方向のとき、給電点における時刻tの電界を式(2-4-1)とします。
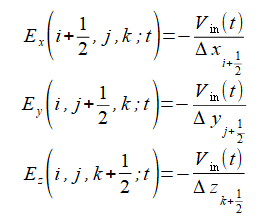(2-4-1)
ここでVは給電電圧であり、その時間波形は次式の微分ガウスパルスとします。
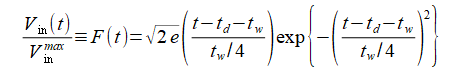(2-4-2)
ここでtwはパルス幅であり、
tdは給電点が複数あるときの位相差を設定するための時間遅れです。
式(2-4-2)は最大値が1になるように正規化されています。
また初期状態(t=0)では給電電圧は十分小さくなっています。
式(2-4-2)は横軸を(t-td)/twとすると図2-4-1のようになります。
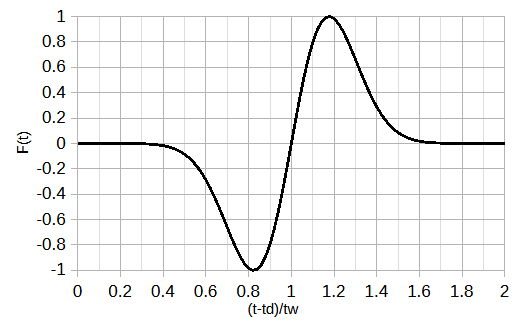
図2-4-1 給電電圧波形
時間波形(2-4-2)のFourier変換は式(2-4-3)となります。
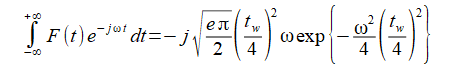(2-4-3)
ここで公式(2-4-4)([7]p.276)の両辺をωで微分した公式(2-4-5)を用いています。
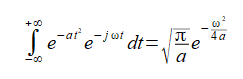(2-4-4)
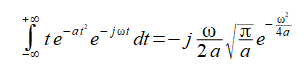(2-4-5)
式(2-4-3)の絶対値を横軸をftwとしてプロットすると図2-4-2のようになります
(縦軸は最大値で正規化しています)。
パルス幅twは式(2-4-3)の絶対値が最大となるように式(2-4-6)とします。
ここでfcは中心周波数です。
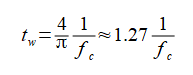(2-4-6)
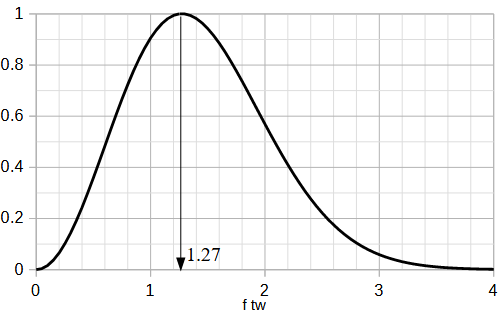
図2-4-2 給電電圧スペクトル
平面波入射モデルでは計算領域の外部から平面波が入射するモデルを考えます。
図2-4-3のように初期状態では計算領域から十分離れた所にパルス状の平面波が存在し、
これが計算領域の方向に入射するものとします。
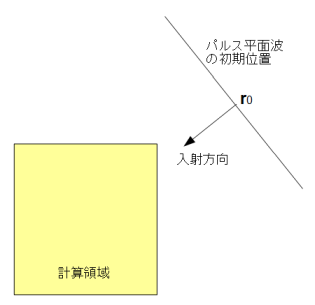
図2-4-3 平面波入射の初期状態
点rにおける時刻tの入射電磁界は次式で表されます。
(r0はパルスの初期位置)
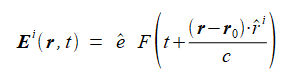(2-4-7)
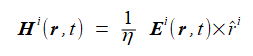(2-4-8)
ここで
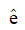は入射電界ベクトルであり、垂直偏波または水平偏波のとき次式で表されます。
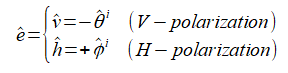(2-4-9)
また
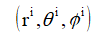を原点から入射方向を見た極座標とすると、各方向の単位ベクトルは次式で表されます。
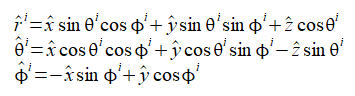(2-4-10)
式(2-4-7)(2-4-8)において、進行方向の単位ベクトルは
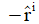であることに注意してください。
また、関数Fは給電点と同じく次式で計算されます。
パルス幅twは式(2-4-6)と同じです。
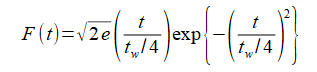(2-4-11)