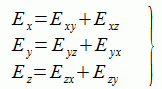 (2-6-1)
(2-6-1)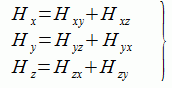 (2-6-2)
(2-6-2)
PML(Berenger's Perfectly Matched Layer)では解析領域の外に余分のセルをとり、
その中でMaxwell方程式を少し変更した方程式をYeeスキームにより計算します。
式(2-6-1)(2-6-2)のように電磁界の各成分を二つの成分に分解します。
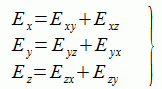 (2-6-1)
(2-6-1)
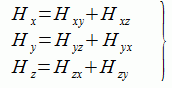 (2-6-2)
(2-6-2)
Maxwell方程式(2-1-4)のXYZ成分を二つに分解すると式(2-6-3)-(2-6-8)になります。
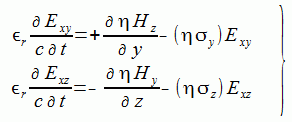 (2-6-3)
(2-6-3)
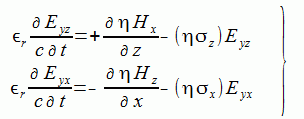 (2-6-4)
(2-6-4)
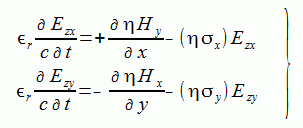 (2-6-5)
(2-6-5)
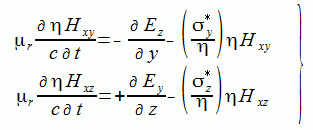 (2-6-6)
(2-6-6)
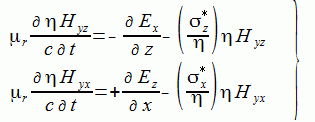 (2-6-7)
(2-6-7)
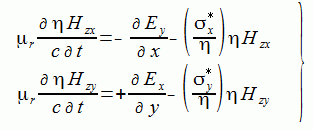 (2-6-8)
(2-6-8)
吸収境界条件(インピーダンス整合条件)は異方性を持った導電率と導磁率に関する以下の式になります。
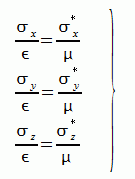 (2-6-9)
(2-6-9)
式(2-6-3)-(2-6-8)をYeeスキームにより離散化すると式(2-6-10)-(2-6-15)となります。
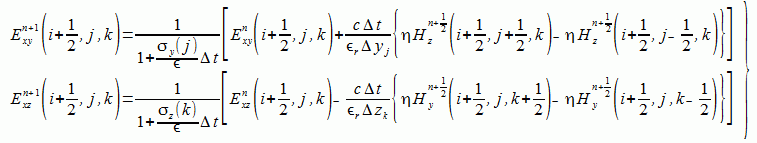 (2-6-10)
(2-6-10)
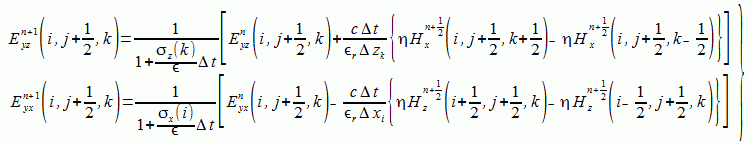 (2-6-11)
(2-6-11)
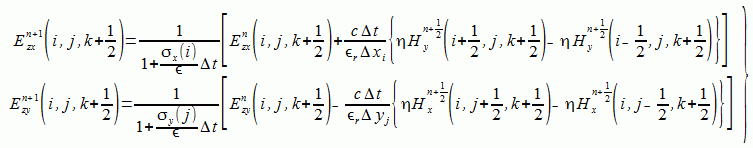 (2-6-12)
(2-6-12)
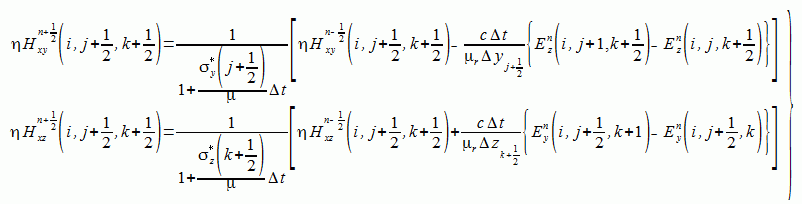 (2-6-13)
(2-6-13)
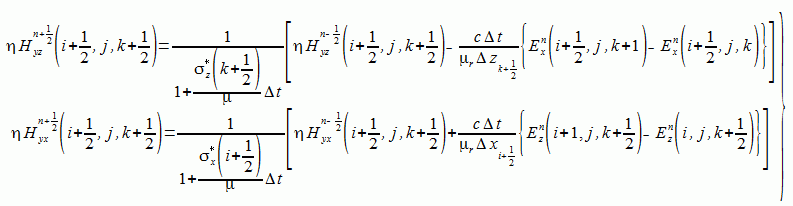 (2-6-14)
(2-6-14)
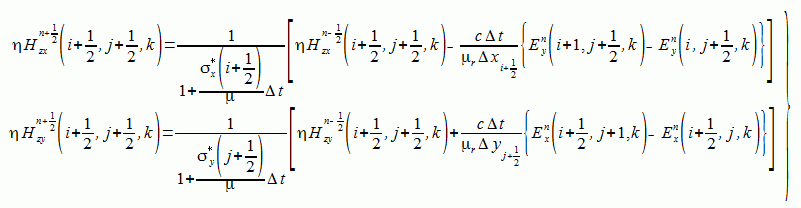 (2-6-15)
(2-6-15)
式(2-6-10)-(2-6-15)の右辺のε,μは境界での値を使用します。
これによって境界にある媒質がその外に無限に続く境界条件を表すことができます。
導電率σは外に行くほど大きくなるように例えば次式の関数形をとります。
(L:PMLの層数、M:正の実数)
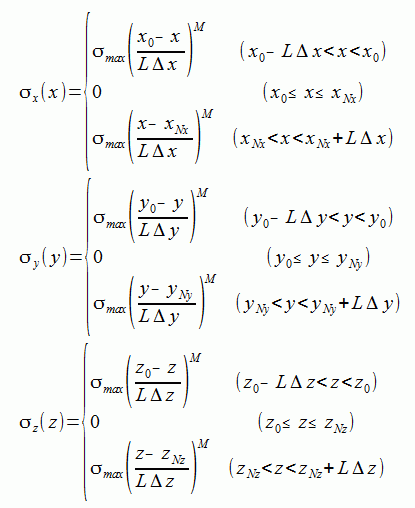 (2-6-16)
(2-6-16)
式(2-6-10)の第一式の分母、および式(2-6-13)の第一式の分母は以下のようになります。
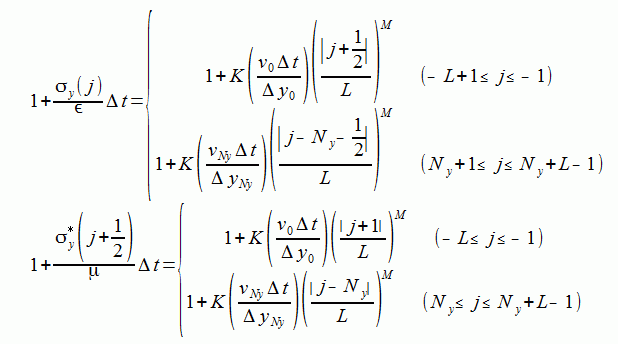 (2-6-17)
(2-6-17)
その他の境界についても同様です。
ここでvは境界での光速、Kは次式で計算される無次元の正の数です。
ただしR0はPML領域の外境界への垂直入射の反射係数です。
ユーザーが指定するパラメータはL,M,R0の三つです
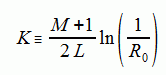 (2-6-18)
(2-6-18)