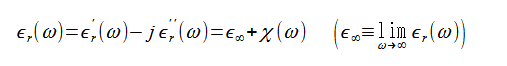(2-8-1)
誘電率が周波数によって変わる媒質を分散性媒質と呼びます。
比誘電率を周波数の関数として次式で表します。
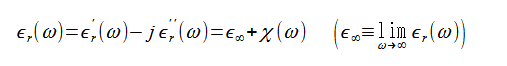(2-8-1)
このときMaxwell方程式(2-1-2)の第1式でσ=0とおいた式は次式のようになります。
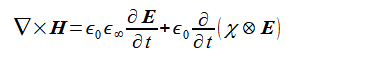(2-8-2)
ここで式(2-8-2)の右辺第2項は次式の畳み込み積分です。
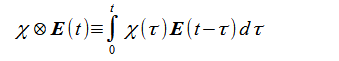(2-8-3)
またχ(t)はχ(ω)の逆Fourier変換です。
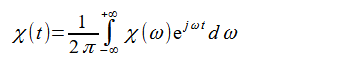(2-8-4)
電磁界を式(2-1-5)のように分解して、
入射電磁界に関する式(2-1-7)第1式を用いると式(2-8-2)は式(2-1-6)第1式に対応して次式のようになります。
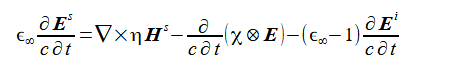(2-8-5)
式(2-8-5)右辺第2項において電界を分解しないことが大切です。
このために、入射波のパルス形状が何であっても解くことができます。
式(2-8-5)を時刻n+1/2で離散化します。
まず、
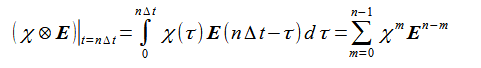(2-8-6)
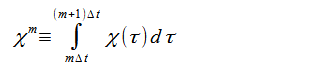(2-8-7)
より、
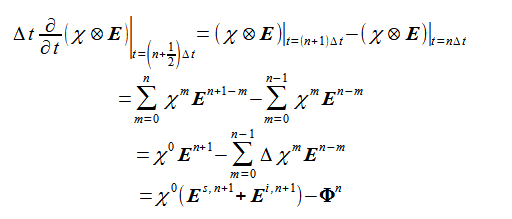(2-8-8)
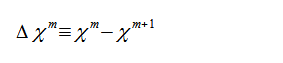(2-8-9)
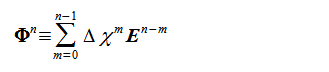(2-8-10)
であるから、式(2-8-5)は、
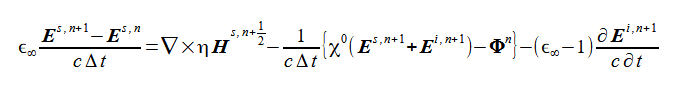(2-8-11)
となり、これをEs,n+1について解くと、次式が得られます。
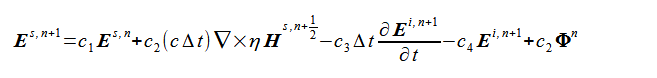(2-8-12)
ここで各係数は次式です。
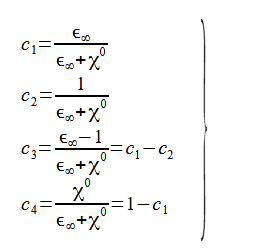(2-8-13)
式(2-8-12)を式(2-3-2)と比べると右辺第5項が加わり、
式(2-8-13)を式(2-3-5)と比べると、
εr→ε∞、
ησcΔt→χ0
と置き換えられることがわかります。
また、波源が平面波入射ではなく給電点のときは式(2-8-12)の右辺第3項と第4項はなくなり、
Es→E、Hs→Hとなります。
透磁率の分散は考えないので磁界を更新する式は(2-3-4)のままです。
前節から分散性媒質と非分散性媒質の違いは式(2-8-12)の右辺第5項ですが、
式(2-8-10)より分散性媒質での過去のすべての電界が必要になりメモリーの観点から実用的ではありません。
ところが分散式が特定の関数式のときは以下で述べるように前1回の電界のみで計算することができます。
(RC法:Recursive Convolution scheme)[1][2]
比誘電率の分散関数として、以下の式を考えます。
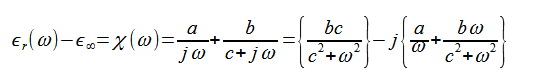(2-8-14)
ここで、a,b,cは定数であり、その次元は[1/s]です。(本節ではcは光速でないことに注意)
式(2-8-14)は特殊な場合として、以下のように1次Debye分散と1次Drude分散を含むので、
ここでは「拡張Debye/Drude分散」と呼びます。
(2-8-15)
以下、式(2-8-14)のときの式(2-8-10)の計算法を述べます。
公式
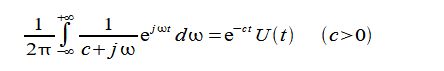(2-8-16)
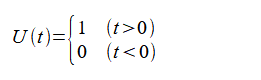(2-8-17)
より、式(2-8-4)は次式になります。
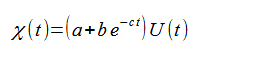(2-8-18)
これより、式(2-8-7)と式(2-8-9)は次式になります。
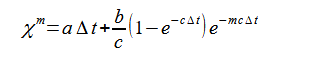(2-8-19)
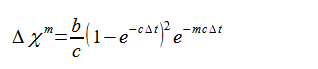(2-8-20)
このとき、
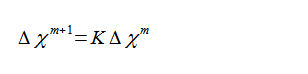(2-8-21)
(2-8-22)
が成り立つので、式(2-8-10)は以下のようになります。
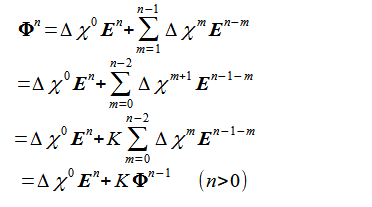(2-8-23)
(2-8-24)
これより、Φnはそのときの電界と前時刻の
Φn-1とから帰納的に計算できます。
必要メモリーは分散性媒質内の電界が2倍になるだけです。
式(2-8-12)(2-8-13)の計算で必要なものは式(2-8-22)と以下のものです。
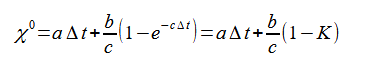(2-8-25)
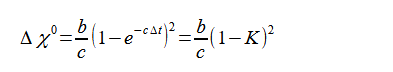(2-8-26)
金と銀の光の領域の複素比誘電率の測定値は文献[12]より図2-8-1のようになります。
この分散は上で述べた拡張Debye-Drude分散式に従わないので、
特定の狭い波長領域で近似した分散パラメーターを使用する必要があります。
任意の各周波数ωにおいて複素比誘電率が与えられたとき、
分散式(2-8-14)を満たす分散パラメーターを求めるには2個の値(εr',εr")
に対して未知数が4個(ε∞,a,b,c)あるので不定ですが、
ここでは狭義の1次Drude分散式(ε∞=1, b=-a)を仮定します。
このとき式(2-8-14)は
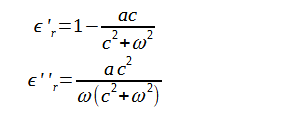(2-8-27)
となり、式(2-8-27)を解くと次式が得られます。
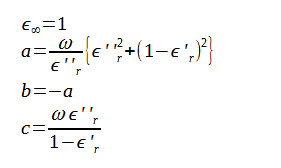(2-8-28)
金と銀の分散パラメーターa,cの波長特性は図2-8-2,2-8-3となり、
その数値は表2-8-1,2-8-2となります。
上で述べたようにこのパラメーターは狭い波長の範囲のみで成り立つ近似なので、
広い範囲の波長を計算するには複数の帯域に分割して計算する必要があります。
なお金銀ともに800nm以上の長波長ではa,cはほぼ一定なので1度で計算することができます。
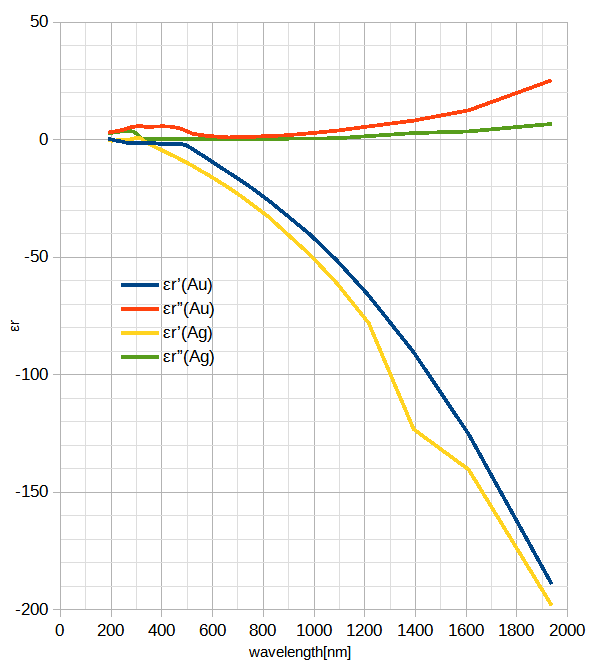
(a)200～2000nm
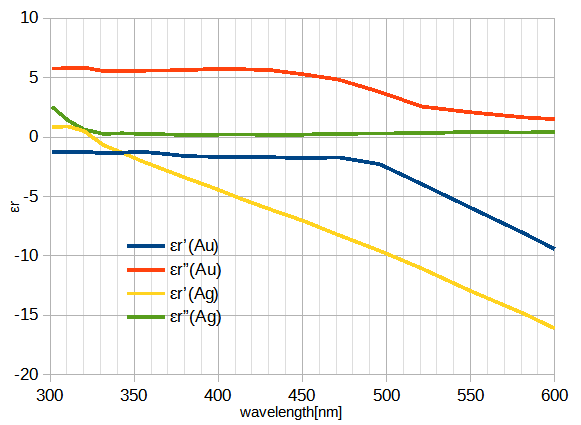
(b)300～600nm(拡大)
図2-8-1 金と銀の複素比誘電率の測定値[12]
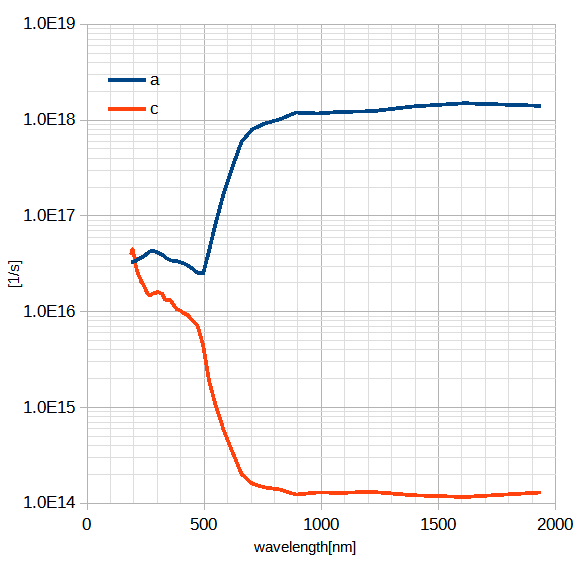
図2-8-2 金の分散パラメーターの波長特性
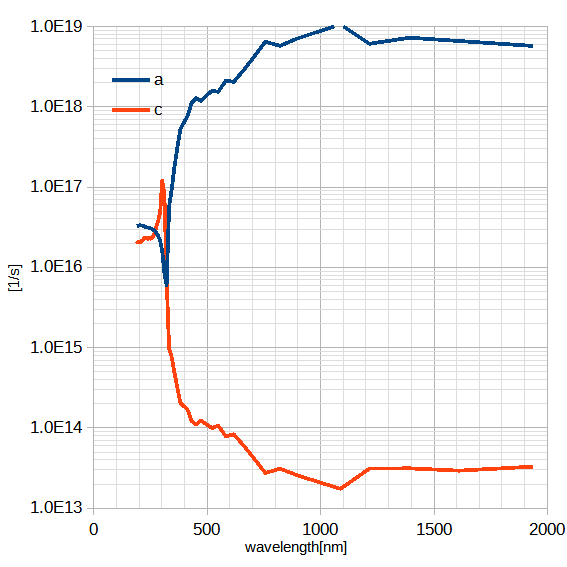
図2-8-3 銀の分散パラメーターの波長特性
表2-8-1 金の分散パラメーターの波長特性
frequency[Hz] wavelength[nm] a[1/s] c[1/s] 1.5475E+14 1937.2695 1.410E+18 1.297E+14 1.8619E+14 1610.1426 1.502E+18 1.162E+14 2.1520E+14 1393.0876 1.392E+18 1.211E+14 2.4664E+14 1215.5062 1.237E+18 1.314E+14 2.7565E+14 1087.5837 1.222E+18 1.285E+14 3.0467E+14 983.9907 1.173E+18 1.296E+14 3.3610E+14 891.9740 1.201E+18 1.231E+14 3.6512E+14 821.0793 1.018E+18 1.392E+14 3.9655E+14 756.0017 9.181E+17 1.466E+14 4.2557E+14 704.4492 7.986E+17 1.601E+14 4.5458E+14 659.4933 5.950E+17 2.019E+14 4.8602E+14 616.8315 3.064E+17 3.598E+14 5.1503E+14 582.0874 1.672E+17 5.897E+14 5.4647E+14 548.5982 8.338E+16 1.060E+15 5.7548E+14 520.9433 4.361E+16 1.886E+15 6.0450E+14 495.9346 2.519E+16 4.417E+15 6.3593E+14 471.4237 2.538E+16 7.162E+15 6.6495E+14 450.8496 2.809E+16 8.000E+15 6.9638E+14 430.5012 3.033E+16 9.181E+15 7.2540E+14 413.2788 3.188E+16 9.644E+15 7.5442E+14 397.3814 3.300E+16 1.027E+16 7.8585E+14 381.4881 3.381E+16 1.070E+16 8.1487E+14 367.9022 3.398E+16 1.196E+16 8.4630E+14 354.2390 3.450E+16 1.334E+16 8.7532E+14 342.4947 3.576E+16 1.318E+16 9.0433E+14 331.5078 3.733E+16 1.345E+16 9.3577E+14 320.3698 3.938E+16 1.541E+16 9.6478E+14 310.7366 4.038E+16 1.566E+16 9.9622E+14 300.9300 4.155E+16 1.624E+16 1.0252E+15 292.4234 4.217E+16 1.563E+16 1.0542E+15 284.3791 4.295E+16 1.561E+16 1.0857E+15 276.1283 4.327E+16 1.523E+16 1.1147E+15 268.9445 4.260E+16 1.485E+16 1.1461E+15 261.5762 4.163E+16 1.521E+16 1.1751E+15 255.1208 4.027E+16 1.594E+16 1.2042E+15 248.9557 3.906E+16 1.736E+16 1.2356E+15 242.6291 3.800E+16 1.853E+16 1.2646E+15 237.0650 3.734E+16 1.993E+16 1.2960E+15 231.3213 3.673E+16 2.043E+16 1.3251E+15 226.2414 3.621E+16 2.250E+16 1.3541E+15 221.3961 3.572E+16 2.345E+16 1.3855E+15 216.3785 3.507E+16 2.544E+16 1.4145E+15 211.9424 3.444E+16 2.755E+16 1.4460E+15 207.3254 3.354E+16 3.049E+16 1.4750E+15 203.2491 3.351E+16 3.653E+16 1.5040E+15 199.3301 3.325E+16 3.950E+16 1.5354E+15 195.2537 3.317E+16 4.480E+16 1.5644E+15 191.6341 3.275E+16 4.429E+16 1.5959E+15 187.8517 3.247E+16 3.946E+16
表2-8-2 銀の分散パラメーターの波長特性
frequency[Hz] wavelength[nm] a[1/s] c[1/s] 1.5475E+14 1937.2695 5.715E+18 3.299E+13 1.8619E+14 1610.1426 6.584E+18 2.941E+13 2.1520E+14 1393.0876 7.230E+18 3.142E+13 2.4664E+14 1215.5062 6.078E+18 3.120E+13 2.7565E+14 1087.5837 1.059E+19 1.749E+13 3.0467E+14 983.9907 8.517E+18 2.147E+13 3.3610E+14 891.9740 6.976E+18 2.611E+13 3.6512E+14 821.0793 5.720E+18 3.110E+13 3.9655E+14 756.0017 6.426E+18 2.752E+13 4.2557E+14 704.4492 4.116E+18 4.240E+13 4.5458E+14 659.4933 2.836E+18 6.070E+13 4.8602E+14 616.8315 2.040E+18 8.343E+13 5.1503E+14 582.0874 2.117E+18 7.861E+13 5.4647E+14 548.5982 1.533E+18 1.066E+14 5.7548E+14 520.9433 1.580E+18 9.977E+13 6.0450E+14 495.9346 1.372E+18 1.112E+14 6.3593E+14 471.4237 1.187E+18 1.242E+14 6.6495E+14 450.8496 1.277E+18 1.102E+14 6.9638E+14 430.5012 1.108E+18 1.221E+14 7.2540E+14 413.2788 7.645E+17 1.680E+14 7.5442E+14 397.3814 6.400E+17 1.858E+14 7.8585E+14 381.4881 5.307E+17 2.058E+14 8.1487E+14 367.9022 3.100E+17 3.175E+14 8.4630E+14 354.2390 1.705E+17 5.024E+14 8.7532E+14 342.4947 9.152E+16 7.699E+14 9.0433E+14 331.5078 5.703E+16 9.659E+14 9.3577E+14 320.3698 6.026E+15 7.503E+15 9.6478E+14 310.7366 8.485E+15 8.226E+16 9.9622E+14 300.9300 1.621E+16 1.210E+17 1.0252E+15 292.4234 2.114E+16 5.000E+16 1.0542E+15 284.3791 2.430E+16 3.873E+16 1.0857E+15 276.1283 2.672E+16 3.268E+16 1.1147E+15 268.9445 2.829E+16 2.712E+16 1.1461E+15 261.5762 2.930E+16 2.449E+16 1.1751E+15 255.1208 3.009E+16 2.335E+16 1.2042E+15 248.9557 3.060E+16 2.270E+16 1.2356E+15 242.6291 3.098E+16 2.301E+16 1.2646E+15 237.0650 3.124E+16 2.260E+16 1.2960E+15 231.3213 3.168E+16 2.351E+16 1.3251E+15 226.2414 3.185E+16 2.314E+16 1.3541E+15 221.3961 3.243E+16 2.305E+16 1.3855E+15 216.3785 3.287E+16 2.189E+16 1.4145E+15 211.9424 3.310E+16 2.148E+16 1.4460E+15 207.3254 3.331E+16 2.117E+16 1.4750E+15 203.2491 3.335E+16 2.036E+16 1.5040E+15 199.3301 3.327E+16 2.067E+16 1.5354E+15 195.2537 3.311E+16 2.054E+16 1.5644E+15 191.6341 3.284E+16 2.037E+16 1.5959E+15 187.8517 3.278E+16 1.964E+16