4. FDTDプログラムの高速化

4.1 ベンチマーク問題

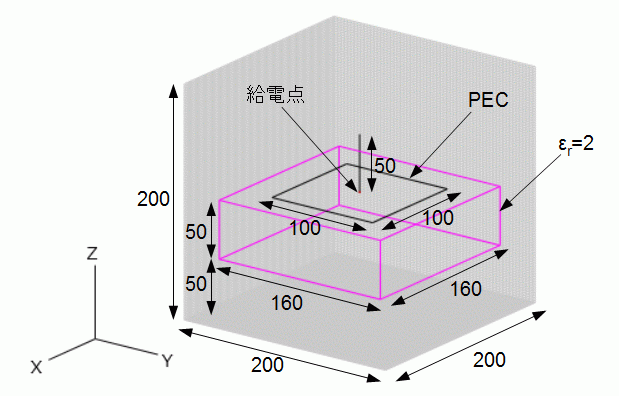
4.1.1 ベンチマーク問題

本章では前章で説明したFDTDプログラムに[3]の高速化技術を適用します。
下記のベンチマーク問題を計算し、その計算時間から高速化を評価します。
計算モデルは図4-1-1の通りです。誘電体のブロックの上に完全導体(PEC)の板があり、その中心にモノポールアンテナが立っているものです。

図4-1-1 ベンチマーク問題(単位:mm)

計算条件として表4-1-1の各ケースを考えます。以下ベンチマーク100～500と呼びます。

表4-1-1 ベンチマーク問題
ベンチマーク	セル数(Nx,Ny,Nz)	セルサイズ(Δx,Δy,Δz)	周波数	タイムステップ数	吸収境界条件	使用メモリー
100	100 X 100 X 100	2X2X2[mm]	10GHz	2000	Mur 1次	30MB
200	200 X 200 X 200	1X1X1[mm]	20GHz	2000	Mur 1次	240MB
300	300 X 300 X 300	0.666X0.666X0.666[mm]	30GHz	2000	Mur 1次	810MB
400	400 X 400 X 400	0.5X0.5X0.5[mm]	40GHz	2000	Mur 1次	1920MB
500	500 X 500 X 500	0.4X0.4X0.4[mm]	50GHz	2000	Mur 1次	3750MB

4.1.2 テスト環境

以下の環境で計算時間を測定します。
全体の計算時間（ofd.logのtotal行）を表示します。

CPU : AMD Ryzen 7 7840HS (8コア16スレッド, 3.8GHz, 最大5.1GHz, L2:8MB, L3:16MB)
GPU : NVIDIA GeForce RTX 4060 Laptop (3072コア, メモリー8GB GDDR6, C.C.8.9)
メモリー : 8GB x 2 (DDR5, 4800MT/s)
OS : Windows 11 23H2
C/C++コンパイラー : Microsoft Visual Studio Community 2022
MPI : Microsoft MPI v10.1.3
CUDA : Version 12.5

4.1.3 二つのモード

電磁界を更新する式には式(2-3-5)(2-3-6)のようにその場所の物性値で決まる4個の係数（c₁,c₂,d₁,d₂）があります。これらを扱うには以下の二通りの方法があります。
(1) novectorモード
その場所の物性値番号（1バイト）から間接的に係数を計算します。使用メモリーが少なくてすみます。
(2) vectorモード
係数の配列（単精度のとき各4バイト）を予め用意し直接アクセスします。使用メモリーが増えます。