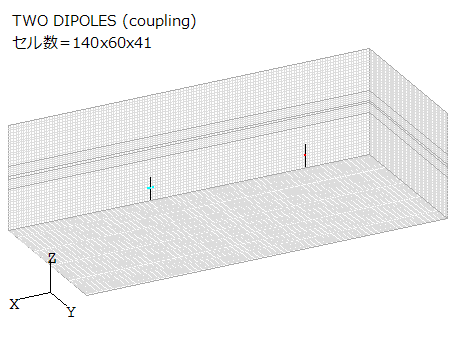
図1 アンテナ結合度の計算モデル
2つのアンテナ間の結合度とFriisの伝達公式を比較します。
結合度の計算式は2.13(4)の通りです。
図1は2つのダイポールアンテナの計算モデルです。
一方のダイポールアンテナを中心で給電し、
他方のダイポールアンテナの中心にギャップを設け、
そこに整合抵抗75Ωと観測点を置きます。
周波数は300MHz(λ=1m)、アンテナ間の距離は3m、
アンテナの長さはどちらも共振長(半波長より少し短い0.42m)とします。
また、結合度を精度よく計算するためには、解析領域をやや大きめにとり、
吸収境界条件はPMLを指定する必要があります。

図1 アンテナ結合度の計算モデル
2つのアンテナ間のFriisの伝達公式は以下のようになります。
Pr / Pt = Gt Gr (λ/(4πd))^2
ここで、Pt:送信電力、Pr:受信電力、d:アンテナ間の距離、
Gt:送信アンテナ利得、Gr:受信アンテナ利得です。
この式に、d=3m、f=300MHz(λ=1m)、Gt=Gr=1.618(=2.089dB) を代入すると、
Pr / Pt = 1.618^2 * (1/(4π*3))^2 = 1.842e-3 = -27.347dB
となります。ここでアンテナ利得は送信アンテナ単体を計算して遠方界から得たものです。
一方、上の計算モデルをOpenFDTDで計算すると、
ofd.logの"coupling"に300MHzで C11=-27.568dBと表示されます。
以上から、アンテナ結合度はFriisの伝達公式(Pr/Pt)とよく一致することがわかります。
参考までに図2に200~400MHzの結合度を示します。
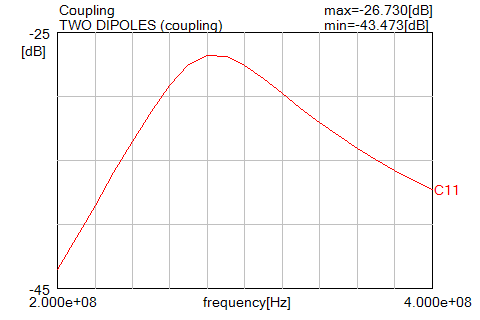
図2 結合度 (200~400MHz)
◆入力データ:
dipole_couple_3m.ofd