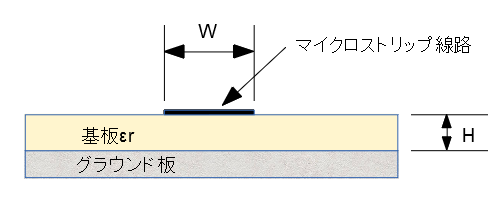
図1 マイクロストリップ線路断面図
マイクロストリップ線路の特性インピーダンスについて考えます。
図1にマイクロストリップ線路の断面図を示します。
線路の厚みと損失を考えないとき、
線路の実効比誘電率εr,effと特性インピーダンスZ0[Ω]は式(1)になります。[11]
(文献[11]の表3.1には2箇所誤りがあるので注意)

図1 マイクロストリップ線路断面図
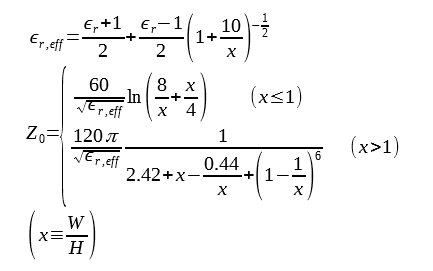 (1)
(1)
下記はマイクロストリップ線路の特性インピーダンスと実効比誘電率を計算するツールです。
3個のデータを入力して[計算]ボタンをクリックしてください。
・基板の比誘電率εr:
・線路の幅W[mm]:
・基板の厚さH[mm]:
式(1)を基板の比誘電率εrをパラメーターにしてグラフにすると図2になります。
図3に特性インピーダンスが50Ωになる線幅W/Hをプロットします。
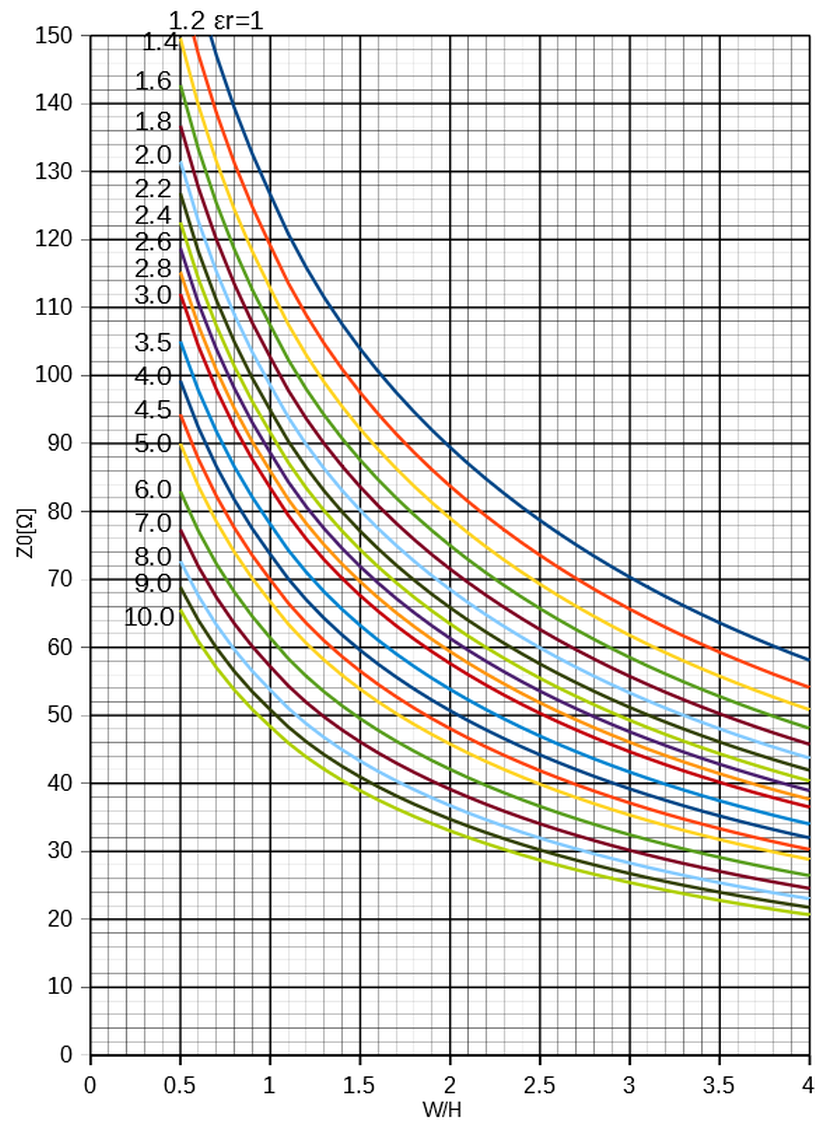
図2 マイクロストリップ線路の特性インピーダンス
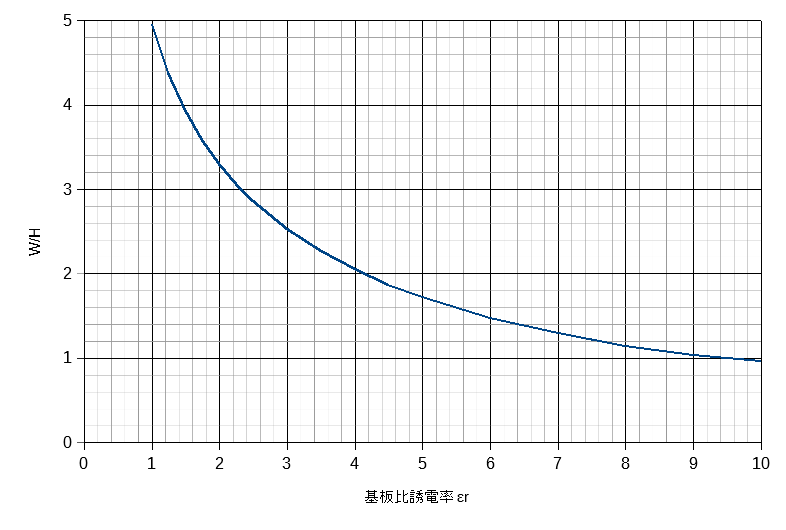
図3 特性インピーダンスが50Ωになる線幅
なお、基板に損失があるときの誘電損失は次式の通りです。(λの単位はm、fの単位はGHz)
従って、tanδが周波数によらないならば誘電損失は周波数に比例します。
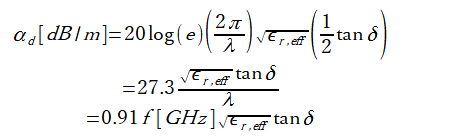 (2)
(2)
線路の特性インピーダンスは線路断面の電圧と電流からZ0=V/Iで定義されますが、
FDTD法では直接計算することが難しいので図4のようなモデルを考えます。
線路を途中で切断してグラウンド板と接続し、その上に給電点を置きます。
このときの入力インピーダンス(Zin=Vin/Iin)
を線路の特性インピーダンスと考えます。これをBlochインピーダンスと呼びます。
図5にセルサイズを変えたときの特性インピーダンスと式(1)の結果を示します。
セルサイズ→0のとき式(1)に収束することがわかります。
これから特性インピーダンスを1Ω以内の誤差で計算するには基板をおよそ10分割以上する必要がありますが、
それはかなり多くの計算時間とメモリーを必要とします。
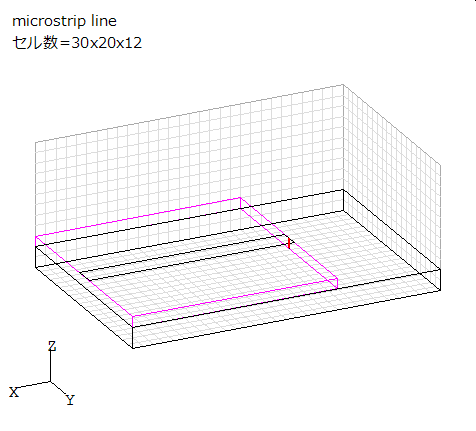
図4 マイクロストリップ線路の計算モデル
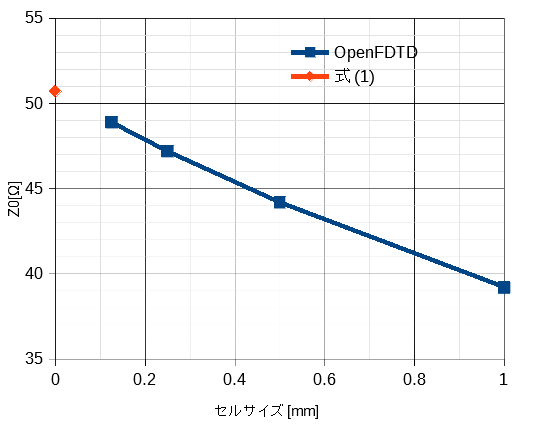
図5 数値解と解析解の比較 (εr=4, W=2mm, H=1mm)
◆入力データ(右クリック+[保存]):
MSL.ofd