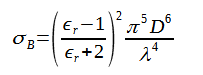 (1)
(1)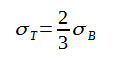 (2)
(2)
図1のように金または銀のナノ粒子を1個配置し、これに平面波が入射するモデルを考えます。
球の直径D=20nmとします。
このとき、球の上には偏波方向に平行な微小電気ダイポールが生じます。
その後方散乱断面積と全散乱断面積は式(1)(2)のレーリー散乱公式で表されます。
式(2)の係数2/3は微小ダイポールのためです。
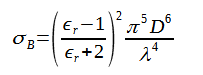 (1)
(1)
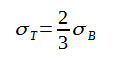 (2)
(2)
各周波数ごとに表2-8-1,2-8-2から分散パラメーターを与えて繰り返し計算します。
図2に金と銀の全散乱断面積の波長特性を示します。
図からレイリー公式と計算値はよく一致しています。
わずかに見られる差は計算誤差その他の要因によります。
金では520nm付近に緩やかなピークが、銀では360nm付近に大きなピークが見られます。
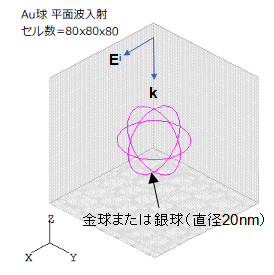
図1 1粒子計算モデル
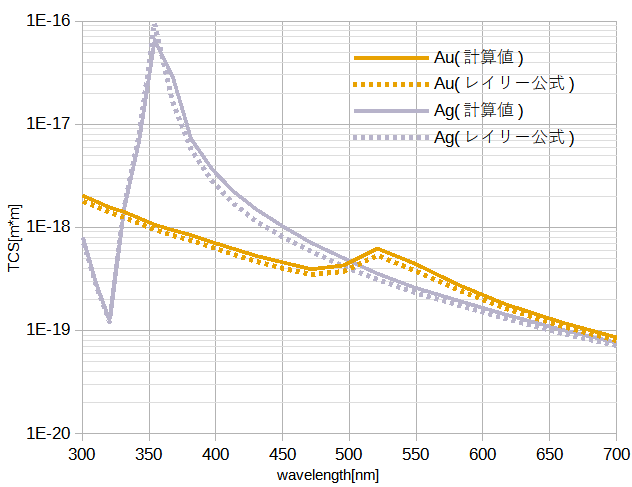
図2 金銀粒子の全散乱断面積の波長特性(D=20nm)
◆入力データ(725THz用)とデータ作成ライブラリー用ソースコード:
Au1_19.ofd
Au1.c
Au_dispersion.h
Ag1_19.ofd
Ag1.c
Ag_dispersion.h
図3のように金または銀のナノ粒子を2個配置し上から平面波が入射するモデルを考えます。
球の直径=20nm、球の間隔=1nm、偏波方向=X方向とします。
波長(周波数)と分散パラメーターは図2-8-2,2-8-3から以下の通りとします。
金: 520nm(577THz), a=4e16[1/s], c=2e15[1/s], ε∞=1, b=-a
銀: 370nm(811THz), a=3e17[1/s], c=3e14[1/s], ε∞=1, b=-a
図4、図5に電界分布を示します。
ギャップの中心に大きな電界が発生します。
その大きさは入射電界と比べて金では34倍、銀では225倍です。
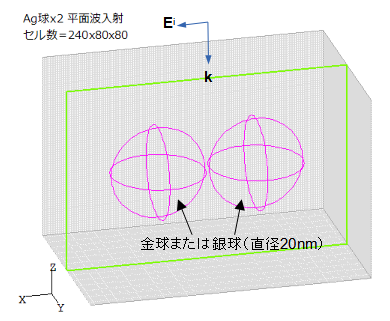
図3 2粒子計算モデル
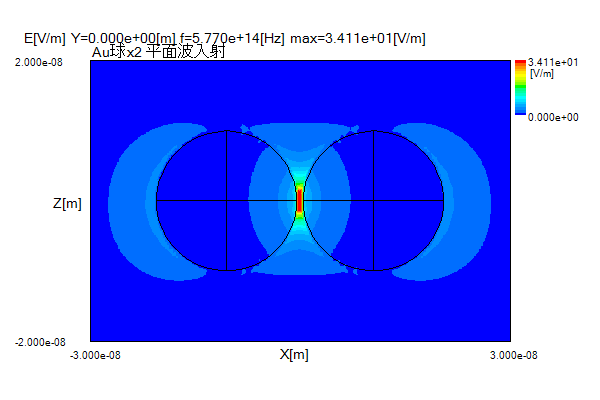
図4 2金球の電界分布(λ=520nm, Y=0面)
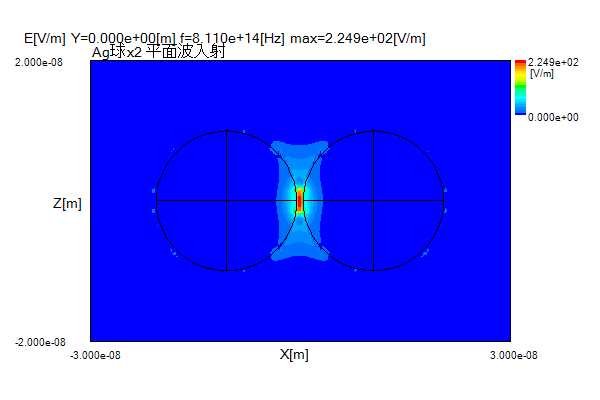
図5 2銀球の電界分布(λ=370nm, Y=0面)
図6に金1粒子の形状を変えたときの後方散乱断面積の波長特性を示します。
形状は直径20nmと40nmの球、および40x20x20nmの楕円体です。
図から球のときは波長特性の形は変わらず後方散乱断面積は直径の6乗に比例します。
これは式(1)の通りです。
一方形が球から変わると波長特性のピークが長波長側にシフトします。
いろいろ形状を変えて計算すると、
入射波の電気ベクトルの方向に細長いときにもっとも大きくシフトすることがわかります。
以上から、後方散乱断面積の波長特性を見ることによって、
ナノ粒子の形状を推定することができます。
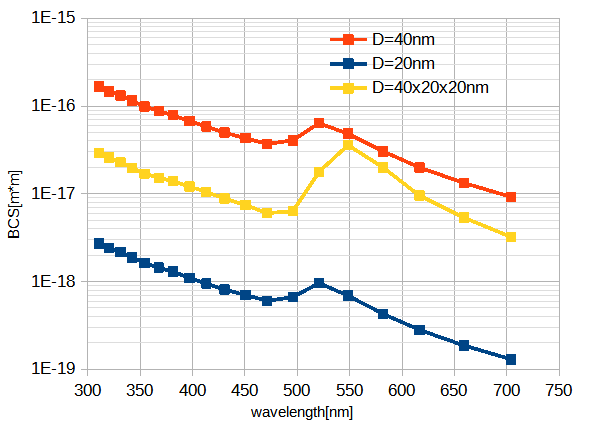
図6 金1粒子の後方散乱断面積と形状の関係