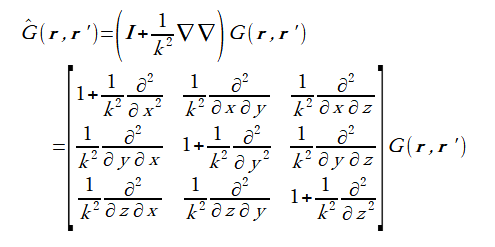(A-1)
式(3-1)のG^をテンソルグリーン関数[1]、
またはダイアディックグリーン関数([16]p.779)と呼びます。
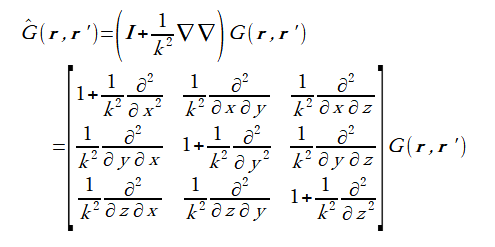(A-1)
ここで右辺のGをスカラーグリーン関数と呼び、次式で表されます。
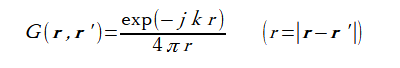(A-2)
式(A-2)をpで微分すると以下のようになります。
以下、p,qはx,y,zのいずれかを表します。
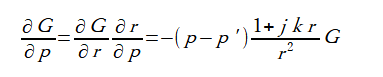(A-3)
公式(A-4)を利用して式(A-3)をqで微分すると式(A-5)が得られます。
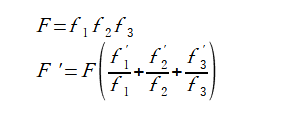(A-4)
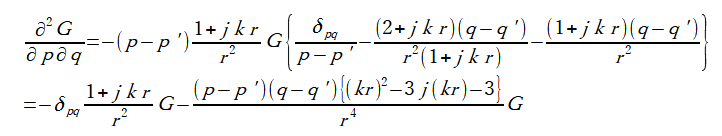(A-5)
以上から式(A-6)が得られます。式(A-6)は無次元量です。
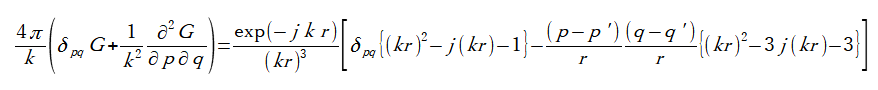(A-6)
式(A-6)からテンソルグリーン関数の各小行列の非対角要素が計算されます。
テンソルグリーン関数の各小行列の対角要素については、
主値をとると異なる成分(p≠q)では0になり、
同じ成分では以下の式から計算されます。
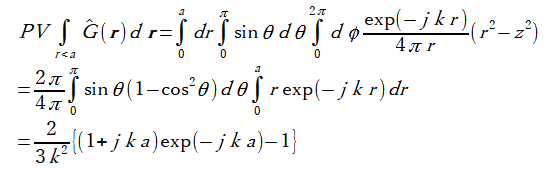(A-7)