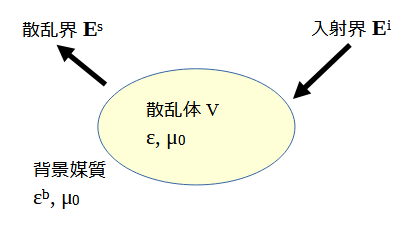
図3-1のように散乱体に電磁波が入射し散乱されるモデルを考えます。
背景媒質は空気以外も想定して誘電率をεbとします。
また磁性体は考えずに透磁率はすべてμ0とします。
散乱体の誘電率εは一般に場所の関数です。

順問題と逆問題の流れは以下のようになります。
・順問題:Ei, ε 既知 → Es 計算
・逆問題:Ei, Es 既知 → ε 計算
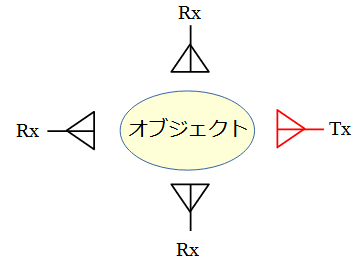
順問題では図3-2のようにオブジェクト(散乱体、対象物)
の周囲に複数のアンテナを置き、一つのアンテナから送信して、
その他のアンテナで受信します。同様にして送信アンテナを切り替えます。
これによってアンテナ間のSパラメーター(結合度)が得られます。
順問題の方法は二つに分かれます。
モーメント法では、図3-1の系ではテンソルグリーン関数Gを用いて、
次式の体積積分方程式が得られます[1][9]。(PV:主値)
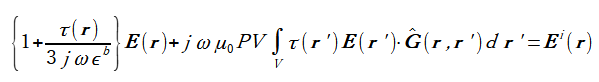 (3-1)
(3-1)
τはコントラストと呼ばれ、
電気定数(jωε)の背景媒質(ε=εb)との差です。
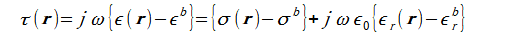 (3-2)
(3-2)
また、Eは次式で表される総合界であり、これが式(3-1)の未知数です。
E = Ei + Es (3-3)
オブジェクト(散乱体)を多数(=N個)のボクセルに分割し、
ボクセル内でEとτは一定として式(3-1)を離散化すると次式のように表されます。
行列は大きさ3N×3Nの正方行列、ベクトルの大きさは3Nです。
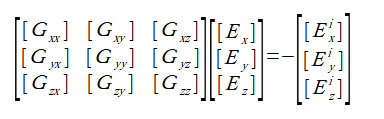 (3-4)
(3-4)
付録Aより、各小行列の非対角成分は式(3-5)、対角成分は式(3-6)となります[1]。
(p,q=x,y,z m,n=1,...,N)
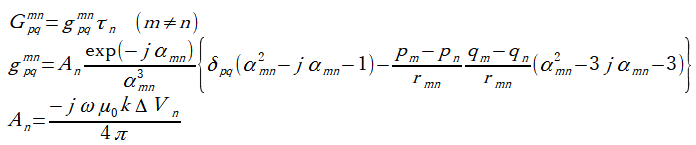 (3-5)
(3-5)
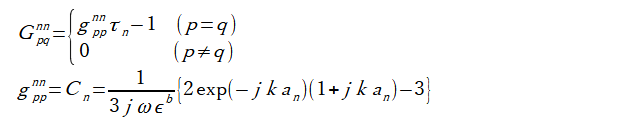 (3-6)
(3-6)
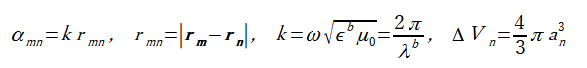 (3-7)
(3-7)
τnはボクセルnのコントラストです。
また、ボクセルの体積が一定ならばAnとCnは定数になります(周波数には依存する)。
式(3-5)(3-6)から逆問題を想定してコントラストを分離し、
MATLAB用に行列で表示すると式(3-4)は以下のようになります。
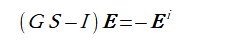 (3-8)
(3-8)
Gは要素gpqmnからなる3N×3Nの行列でコントラストとは無関係、
Sはコントラストτnを3重に並べた3N×3Nの対角線行列、
Iは3N×3Nの単位行列です。
連立一次方程式(3-8)を解くことによってボクセル内の総合界Eが得られます。
なお、式(3-8)の右辺は送信アンテナの放射する電磁界であり既知量です。
微小電流波源の放射電磁界については付録Bを参考にしてください。
上で求めたボクセル内の総合界とコントラストから外部の散乱界が次式で計算されます([1]式(3.26))。
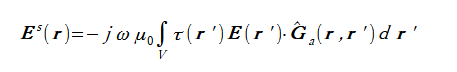 (3-9)
(3-9)
受信アンテナの位置での電界のアンテナの偏波方向の成分がSパラメーターとなります。
テンソルグリーン関数Gaの計算では、
波源と観測点が異なるので対角成分と非対角成分ともに式(3-5)となります。
FDTD法(時間領域差分法)による順問題の計算としてOpenFDTD[10]を使用します。
MATLABでOpenFDTDの入力データを作成し、
system関数を用いてexeファイルを実行します。
ただし、物性値の数が多いためにOpenFDTDはコンパイルオプションに
"D_ID32"をつけて再コンパイルする必要があります。
詳しくはOpenFDTDのページの5.1.5を参考にしてください。
(注意)必要なバグ修正を含んでいるので、バージョン3.1.1以上を使ってください。
一つのアンテナを電圧で給電し、他のアンテナの給電点に整合抵抗を置いて計算すると、
アンテナ間のSパラメーター(結合度)が計算されます。
これが実測値に対応します。
OpenFDTDを用いて順問題を計算するMATLABのソースコードは下記からダウンロードしてください。
forward_fdtd.zip
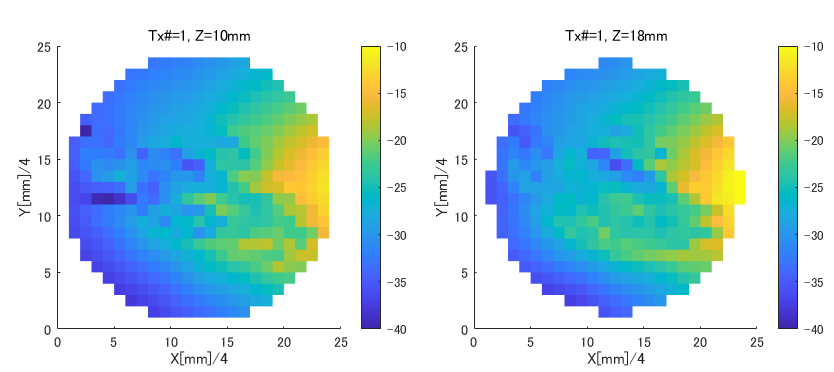
図3-3にモーメント法による電界分布、
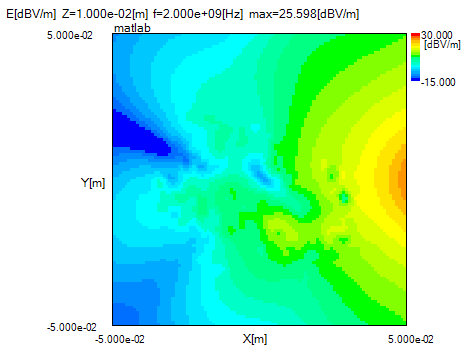
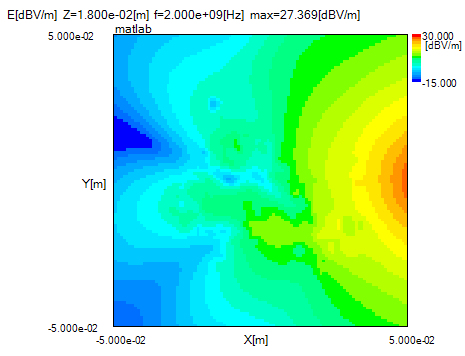
図3-4にFDTD法による電界分布を示します。
いずれも左がZ=10mm面、右がZ=18mm面です。
表示領域は共通で100mm×100mmです。
セルサイズはモーメント法は4mm、FDTD法は1mmです。
計算時間はモーメント法は64秒、FDTD法は18秒(ファイル入出力に40秒)です。
モーメント法では乳房内のみの電界が計算されます。
送信アンテナは図の右辺中央から右に10mm離れた所の高さ25mmの所にZ方向の電流源を置いています。
周波数は2.0GHzです。
乳腺とがんでは導電率が高いために減衰が大きく電界が小さくなります。
図3-3、図3-4ともにその傾向が見られます。
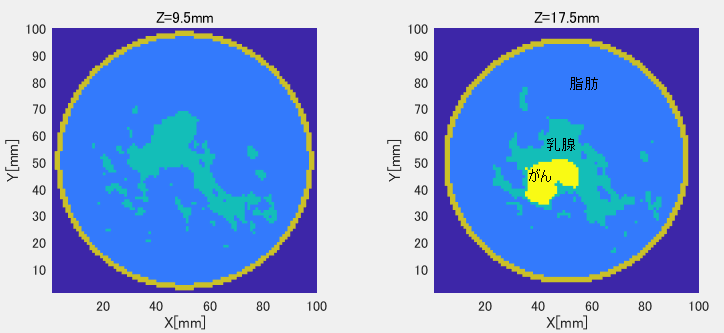
参考までに図3-5に組織図を示します。緑色が乳腺、黄色ががんです。