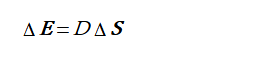 (4-1)
(4-1)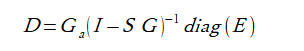 (4-2)
(4-2)
逆問題の計算にはモーメント法とNewton法を用います[1]。
連立一次方程式(3-8)と積分式(3-9)において、
コントラストSの変化量ΔSとSパラメータの変化量ΔEの関係を求めると次式となります([1]式(5.52)。
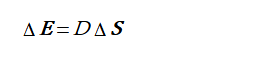 (4-1)
(4-1)
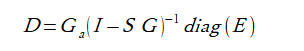 (4-2)
(4-2)
各変数の意味は以下の通りです。括弧内は大きさです。
(N : ボクセル数、Na:アンテナ数)
・ΔE:アンテナのSパラメータの変化量(Na2×1)
・D:Sパラメーターの変化量とコントラストの変化量を関係付ける行列(Na2×3N)
・ΔS:ボクセルのコントラストの変化量を3重に並べたベクトル(3N×1)
・Ga:式(3-9)のテンソルグリーン関数の行列(Na2×3N)
・I:単位行列(3N×3N)
・S:ボクセルのコントラストを3重に並べた対角線行列(3N×3N)
・G:式(3-8)のテンソルグリーン関数の行列(3N×3N)
・diag(E):ボクセルの総合界を並べた対角線行列(3N×3N)
DはコントラストSを含むために式(4-1)は非線形の方程式です。
式(4-1)の両辺にDHをかけて正規化を行うと式(4-3)となります
(H:複素共役転置行列、Hermite転置、随伴行列、共役転置)。
右辺の行列は大きさ3N×3Nの正方行列です。
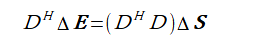 (4-3)
(4-3)
収束を安定化させるためにTikhonovの正則化[11]を行いて式(4-3)を解くと式(4-4)となります。
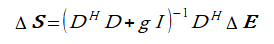 (4-4)
(4-4)
ここでgは経験的に決める微小量です。
なお、連立一次方程式(4-1)において方程式の数(=Na2)が未知数の数(=3N)より多いとき優決定、
少ないとき劣決定と呼びます。
ここでは正確な解を求めるために優決定(Na2>3N)を考えます。
逆問題を解くアルゴリズムは以下のようになります。
収束判定条件としてはΔE→0とΔS→0のどちらでも構いませんが、
方程式が非線形の悪条件であるために、
どちらも0になっても真の解ではなく偽の極小点(偽像、アーティファクト)である可能性があります。
従って正しくは本来未知量である正しいコントラストS0との差を見る必要があります(S→S0)。
後の計算で見るように多くの場合前者が0になるときは後者の差も0になります。
従って前者の収束判定条件で問題ありません。
反復計算におけるコントラストτの初期値としては、
全ボクセルに次式と式(3-2)から計算される一定値を与えます。
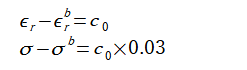 (4-5)
(4-5)
ここで"0.03"は2.2で述べたように組織によらず導電率[S/m]は比誘電率の約3%であることによります。
またc0は定数であり、付録Cからc0=3とします。
式(4-4)の正則化因子gは次式で計算します[1]。
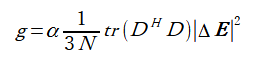 (4-6)
(4-6)
ここでαは経験的に決める微小な定数です。
trは対角成分の和で行列要素の大きさを表します。
ΔEは4.2の5.のSパラメーターの誤差です。
従ってgは最初は大きく、収束が近づくと小さくなります。
付録Cからα=0.01とします。
付録Fに正則化因子gと式(4-4)の行列(DHD+gI)の条件数の逆数の関係を示します。
収束が近づくと条件数が大きくなります。
収束を安定化させるために電気定数に制約条件を設けることができます[1]。
式(4-7)が制約条件の一例です。
コントラストτから比誘電率と導電率を取り出し、
比誘電率は1以上60以下、導電率は比誘電率の2%以上4%以下になるようにした後、
コントラストに戻しています。
制約条件を設けないと発散し、制約条件を設けると収束することがあります。
従って、制約条件は必要です。
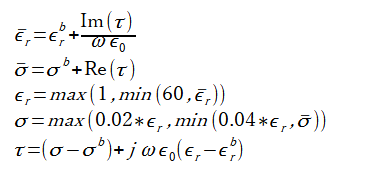 (4-7)
(4-7)