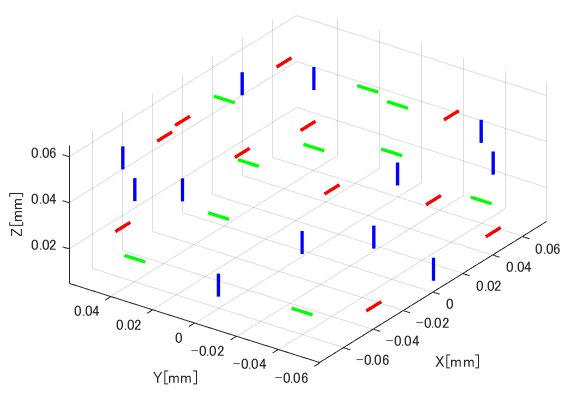
アンテナの配置は図5-1の通りです。
±X面、±Y面、+Z面の5面に等間隔にアンテナを配置します。
隣接するアンテナ間の強い結合はオブジェクトに関する情報を含まない不要な情報なので、
隣接するアンテナの偏波は互いに直交するようにしています。
原点からアンテナ面までの距離はRa=60mmとします。
アンテナの位置と偏波が収束に与える影響は付録Dで考察します。
アンテナ配置のX/Y/Z方向の分割数をnx/ny/nzとすると総アンテナ数Naは次式の通りです。
Na = (nx * ny) + (2 * nz) * (nx + ny) (5-1)

モーメント法は計算時間がかかるために、
元の数値ファントムのボクセルを合体して一つのボクセルとしています。
合体する数をHとします。
例えばH=6のときは、
63=216個のボクセルの比誘電率と導電率の平均を合体したボクセルの値としています。
計算を開始すると、最初に順問題を計算し、その後逆問題を反復計算します。
図5-2に逆問題の誤差の収束状況の一例を示します。
横軸は反復回数で、グラフの5本の線の意味は以下の通りです。
(1) ΔE/E : Sパラメーターの変化量と現在のSパラメーターの比
(2) Δεr/εr : 比誘電率の変化量と現在の比誘電率の比
(3) Δσ/σ : 導電率の変化量と現在の導電率の比
(4) (εr-εr0)/εr0 : 比誘電率の真値との差と比誘電率の真値の比
(5) (σ-σ0)/σ0 : 導電率の真値との差と導電率の真値の比
収束判定条件は次式のように(2)と(3)が十分小さくなることとしています。
Δεr/εr < 10-4, Δσ/σ < 10-4 (5-2)
図5-2からわかるように(2)と(3)が十分小さくなるとその他も同時に十分小さくなります。
(4)と(5)の真値は本来は逆問題では未知量なので使用することはできませんが、
式(5-2)が収束判定条件として十分であることを裏付けています。
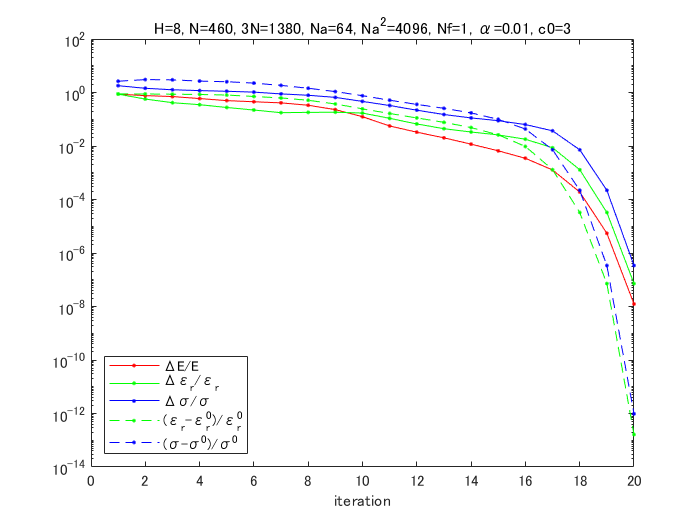
図5-3にコントラストの分布図の一例を示します。
3次元のボクセルを1次元に並べて、数値ファントム(合体後)と計算値を比較したものです。
上が比誘電率、下が導電率です。
(a)は途中経過です。全体に誤差が見られます。
図5-2からもわかるように比誘電率の方が比較的速く収束します。
(b)は収束した状態です。
すべてのボクセルで比誘電率と導電率が数値ファントムに一致します。
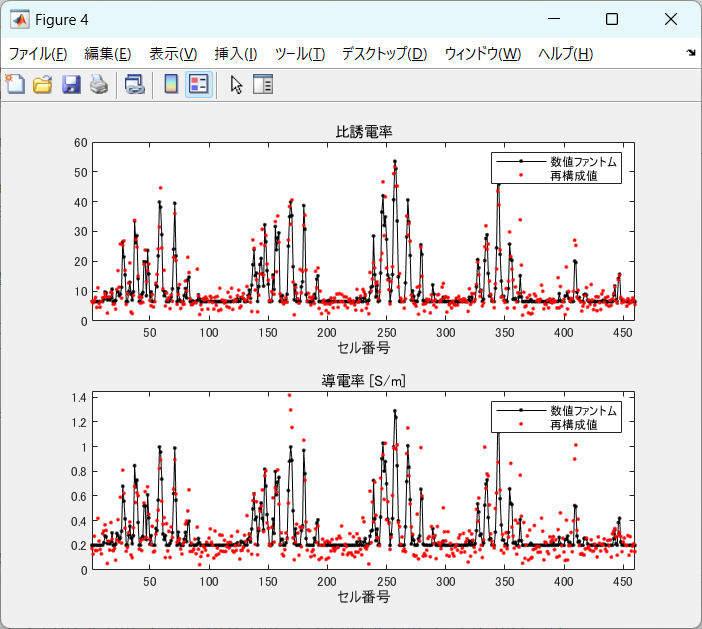
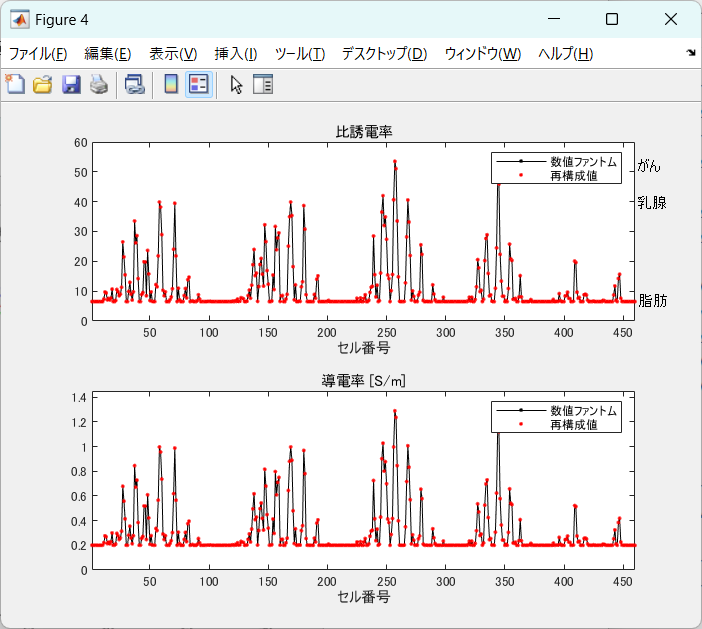
図5-3 コントラスト分布の真の値と計算値の比較
計算環境は以下の通りです。
なお、すべてのCPUコアを使用して並列計算されています。
共通の計算条件は表5-1の通りです。
| パラメーター | 値 |
|---|---|
| 背景媒質 | 脂肪 |
| 容器媒質 | 脂肪 |
| 周波数 | 2.0GHz |
| アンテナ配置 | 5面(±X面、±Y面、+Z面) |
| アンテナ位置Ra | 60mm |
| アンテナ偏波方向 | 交互配置 |
| 正則化パラメーターα | 0.01 |
| 初期値因子c0 | 3 |
| 収束判定条件 | 10-4 |
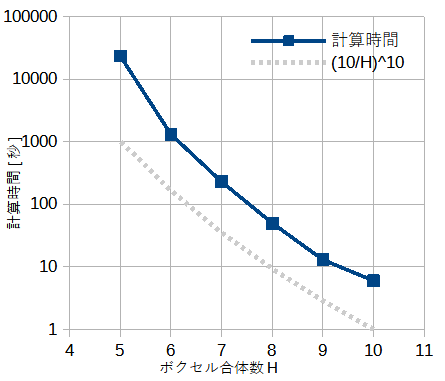
表5-2に各ケースの計算条件と計算結果を示します。
| No. | ボクセル合体数 H | ボクセル総数 N (3N) | アンテナ配置数 (nx,ny,nz) | アンテナ総数 Na (Na2) | 優決定度 Na2/3N | 収束反復回数 | 計算時間 [秒] |
|---|---|---|---|---|---|---|---|
| 1 | 10 | 240 (720) | (4,4,2) | 48 (2304) | 3.20 | 12 | 6 |
| 2 | 9 | 314 (942) | (4,4,2) | 48 (2304) | 2.45 | 16 | 13 |
| 3 | 8 | 460 (1380) | (4,4,2) | 48 (2304) | 1.67 | 94 | 153 |
| 4 | (4,4,3) | 64 (4096) | 2.97 | 20 | 50 | ||
| 5 | (5,5,2) | 65 (4225) | 3.06 | 21 | 54 | ||
| 6 | 7 | 680 (2040) | (4,4,3) | 64 (4096) | 2.01 | 49 | 275 |
| 7 | (5,5,2) | 65 (4225) | 2.07 | 52 | 299 | ||
| 8 | (5,5,3) | 85 (7225) | 3.54 | 28 | 229 | ||
| 9 | (6,6,3) | 108 (11664) | 5.72 | 26 | 311 | ||
| 10 | 6 | 1071 (3213) | (5,5,3) | 85 (7225) | 2.25 | 80 | 1757 |
| 11 | (6,6,3) | 108 (11664) | 3.63 | 45 | 1308 | ||
| 12 | (6,6,4) | 132 (17424) | 5.42 | 36 | 1440 | ||
| 13 | (7,7,4) | 161 (25921) | 8.07 | 33 | 1863 | ||
| 14 | 5 | 1824 (5472) | (7,7,4) | 161 (25921) | 4.74 | 145 | 23345 |
| 15 | (8,8,4) | 192 (36864) | 6.74 | 156 | 36800 |
表5-2から以下のことがわかります。