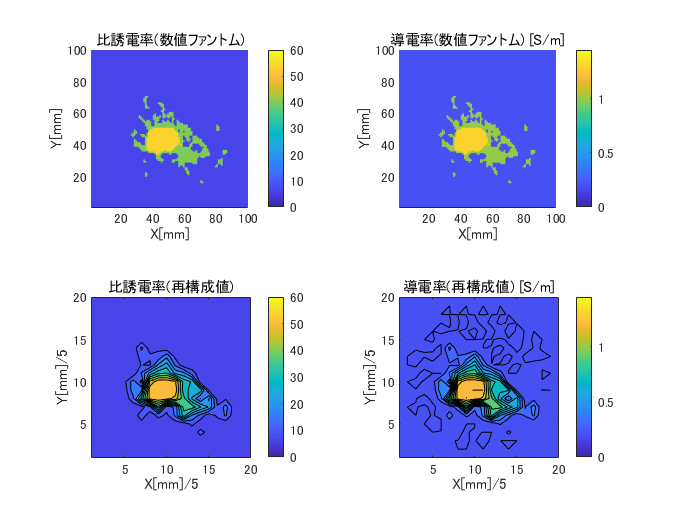
図6-1に計算結果の一例を示します。
Z一定面で、上は合体する前の数値ファントムの比誘電率と導電率の分布図(分解能1mm)、
下は再構成値(逆問題の解)の比誘電率と導電率の分布図です。
比誘電率と導電率は各組織でほぼ比例するために同じような図になります。
従って、以下では比誘電率のみを示します。

図6-2は同じ計算結果の図形出力方法を変えたものです。
図の上に図形出力のコマンドを示します。
同じ計算結果でも印象が変わります。
以下では左上の図形出力方法を採用します。
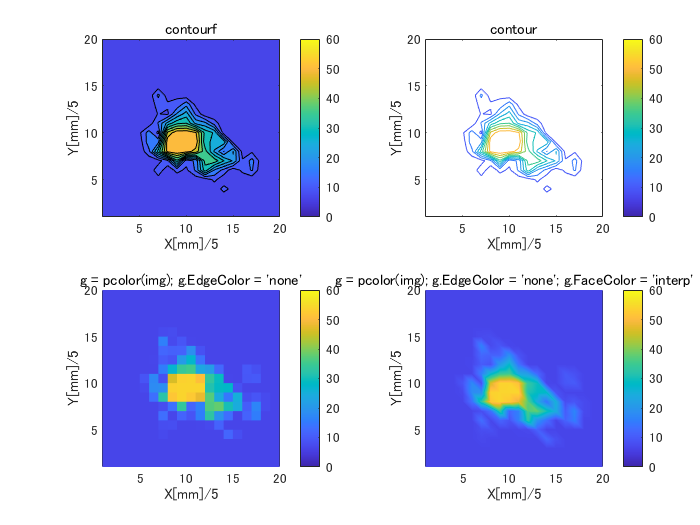
図6-3にcase1のZ面の比誘電率の数値ファントムと再構成値の比較を示します。
上から順にZ=12.5,17.5,22.5,27.5mm面です。
がんのないZ=12.5mm面は乳腺のみの緑色、
がんのあるZ=22.5mm面は黄色のがんが認められます。
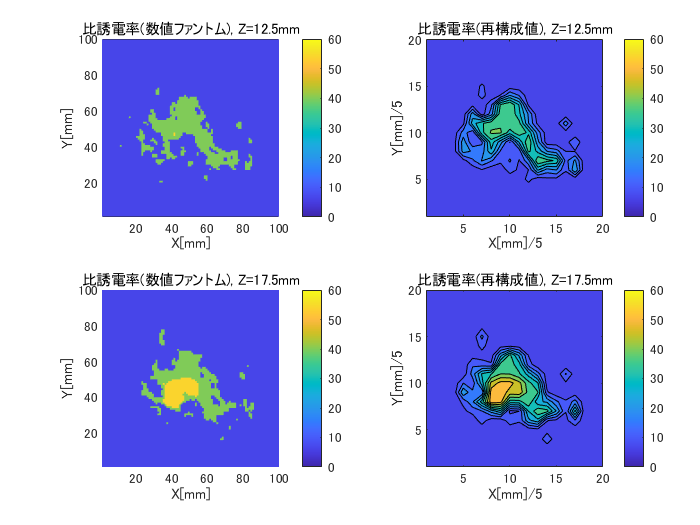
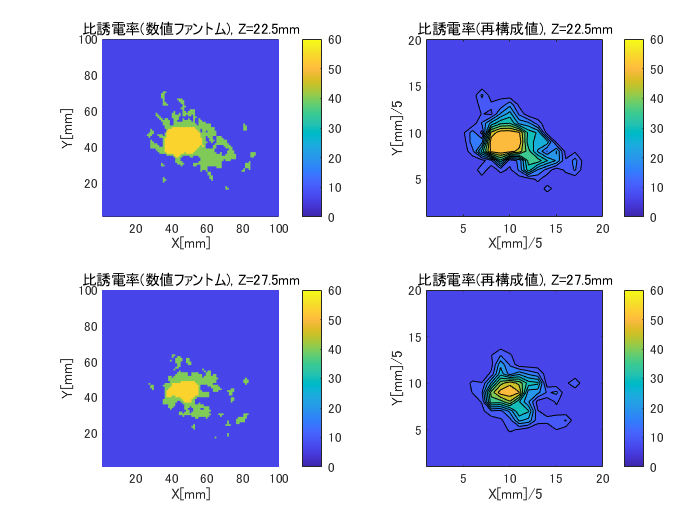
(case1, H=5, (nx,ny,nz)=(7,7,4), Z=12.5~27.5mm面)
図6-4にcase1のX面の比誘電率の数値ファントムと再構成値の比較を示します。
上から順にX=37.5,42.5,47.5,52.5mm面です。
図6-3と同様にがんの有無が判別できます。
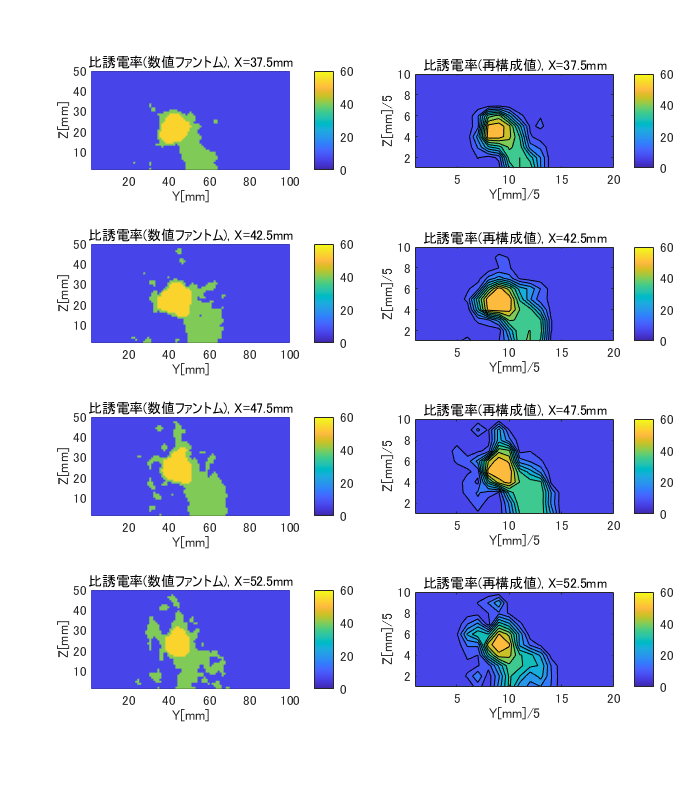
(case1, H=5, (nx,ny,nz)=(7,7,4), X=37.5~52.5mm面)
図6-5にcase1のY面の比誘電率の数値ファントムと再構成値の比較を示します。
上から順にY=37.5,42.5,47.5,52.5mm面です。
図6-3と同様にがんの有無が判別できます。
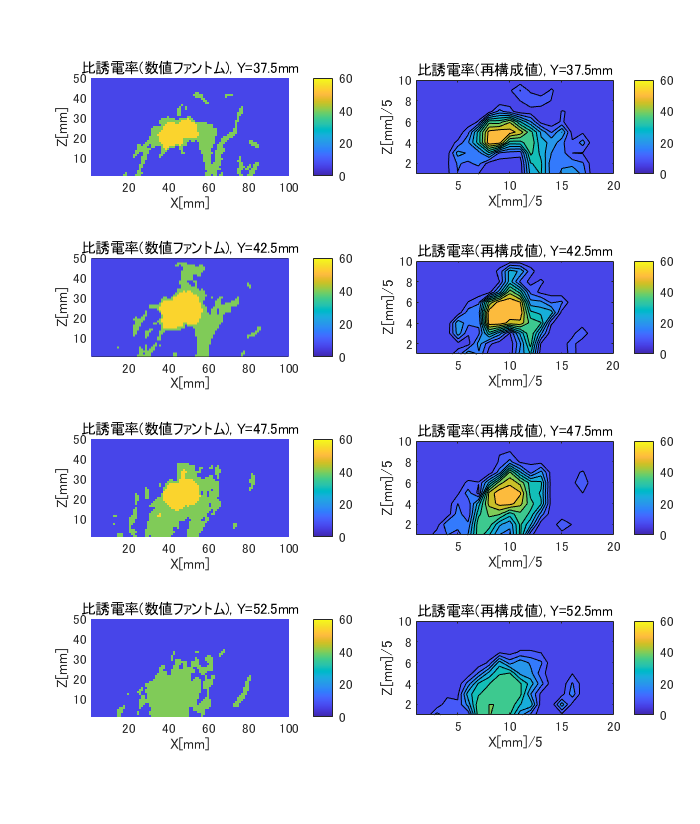
(case1, H=5, (nx,ny,nz)=(7,7,4), Y=37.5~52.5mm面)
図6-6にcase2のZ面の比誘電率の数値ファントムと再構成値の比較を示します。
図6-3と同様にがんの有無が判別できます。
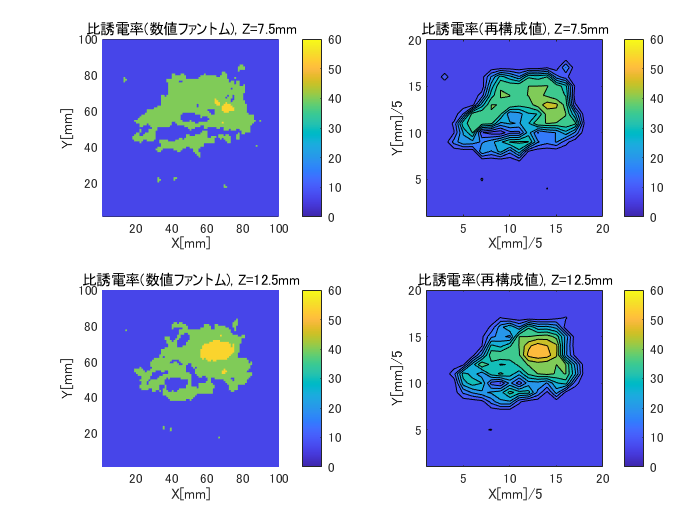
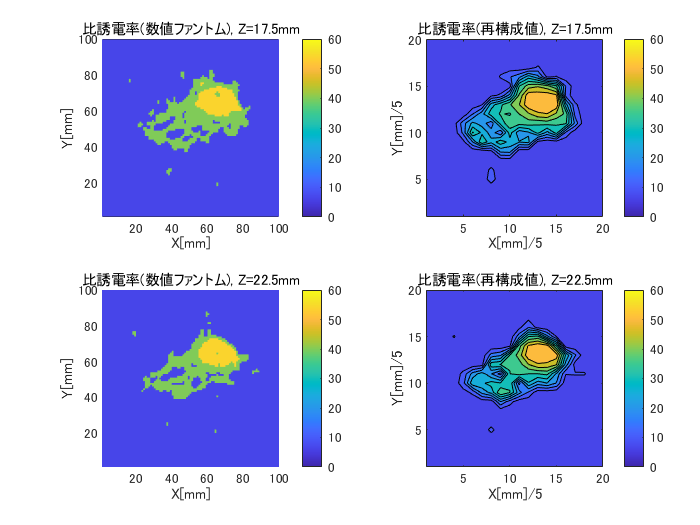
(case2, H=5, (nx,ny,nz)=(7,7,4), Z=7.5~22.5mm面)
図6-7にcase2のX面の比誘電率の数値ファントムと再構成値の比較を示します。
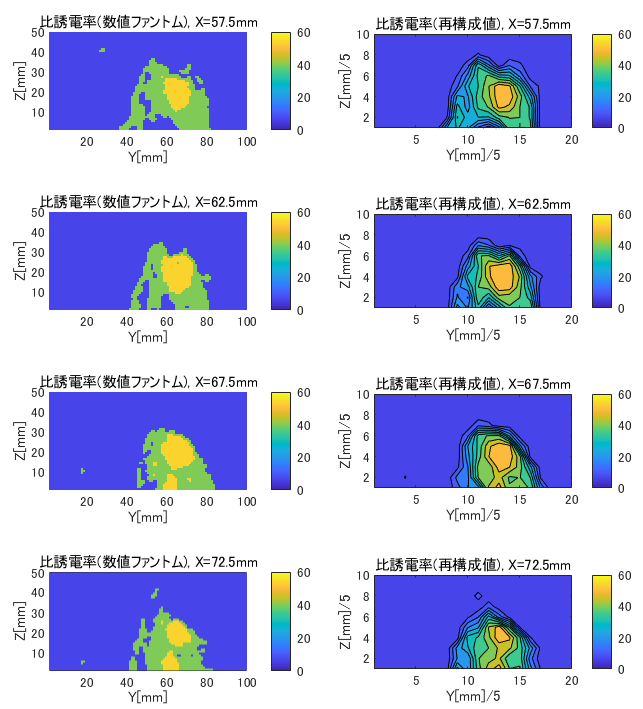
(case2, H=5, (nx,ny,nz)=(7,7,4), X=57.5~72.5mm面)
図6-8にcase2のY面の比誘電率の数値ファントムと再構成値の比較を示します。
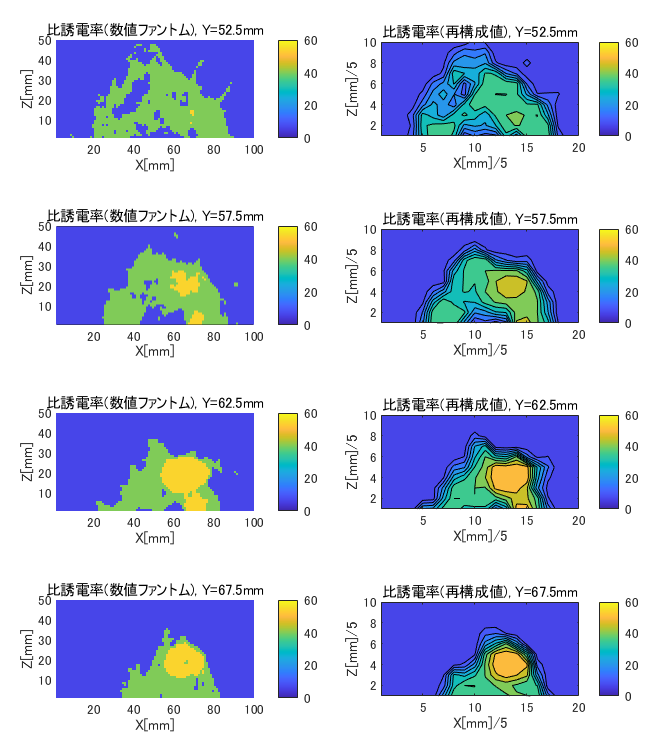
(case2, H=5, (nx,ny,nz)=(7,7,4), Y=52.5~67.5mm面)
図6-9にcase3のZ面の比誘電率の数値ファントムと再構成値の比較を示します。
がんが小さいためにcase1,case2に比べると判別度が落ちます。
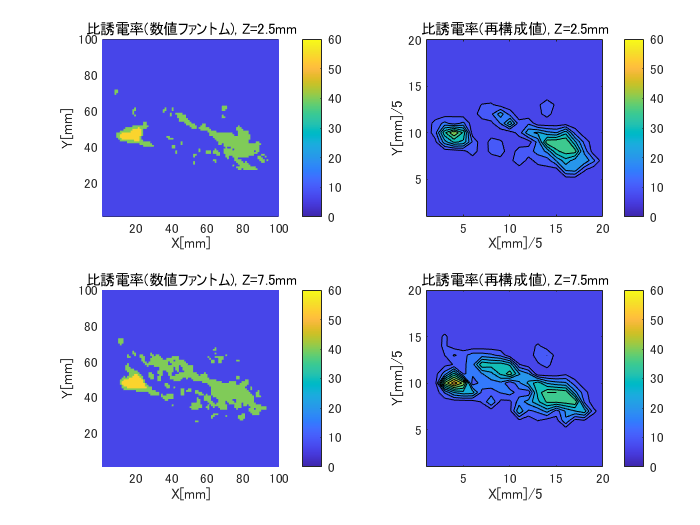
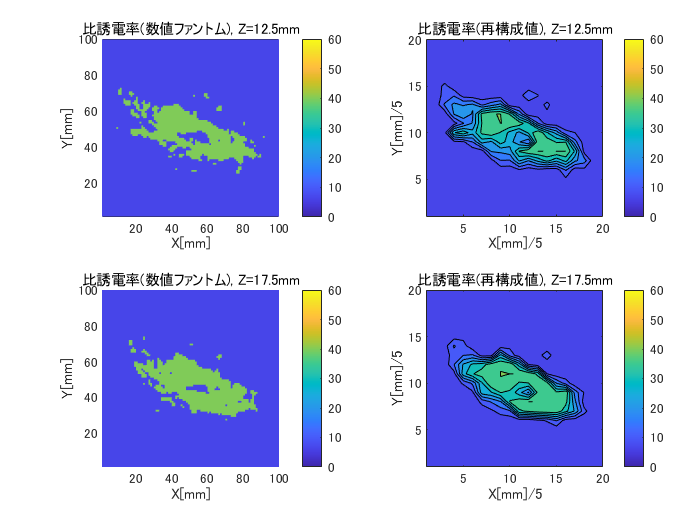
(case3, H=5, (nx,ny,nz)=(7,7,4), Z=2.5~17.5mm面)
図6-10にcase3のX面の比誘電率の数値ファントムと再構成値の比較を示します。
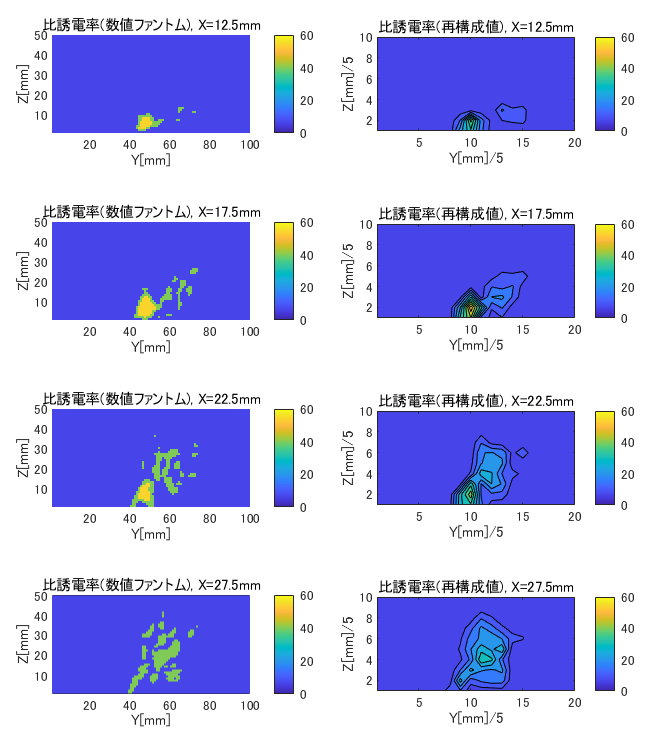
(case3, H=5, (nx,ny,nz)=(7,7,4), X=12.5~27.5mm面)
図6-11にcase3のY面の比誘電率の数値ファントムと再構成値の比較を示します。
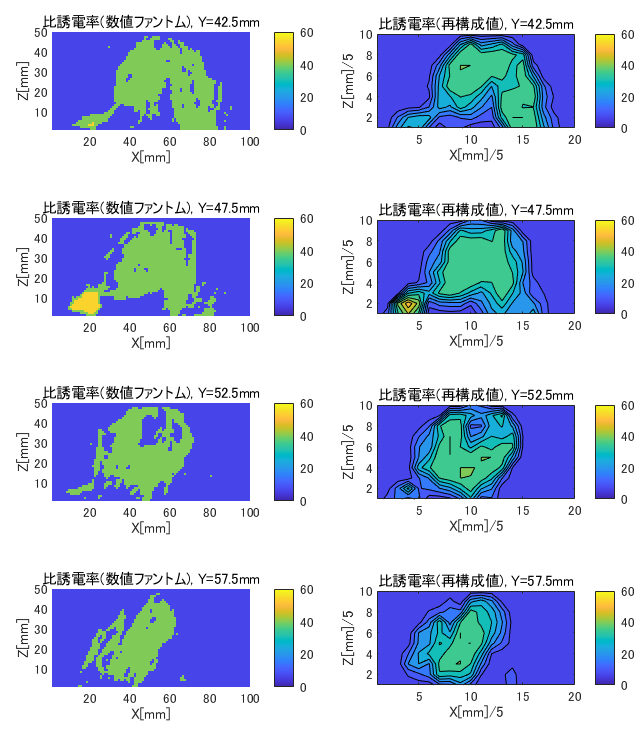
(case3, H=5, (nx,ny,nz)=(7,7,4), Y=42.5~57.5mm面)
図6-12に各ケースの比誘電率の再構成値の頻度分布を示します。
大部分を占める脂肪は比誘電率が小さいので脂肪を除くために横軸の下限を20としています。
がんがあると乳腺の右にピークが現れます。
case3はがんが小さいのでピークが不明瞭です。
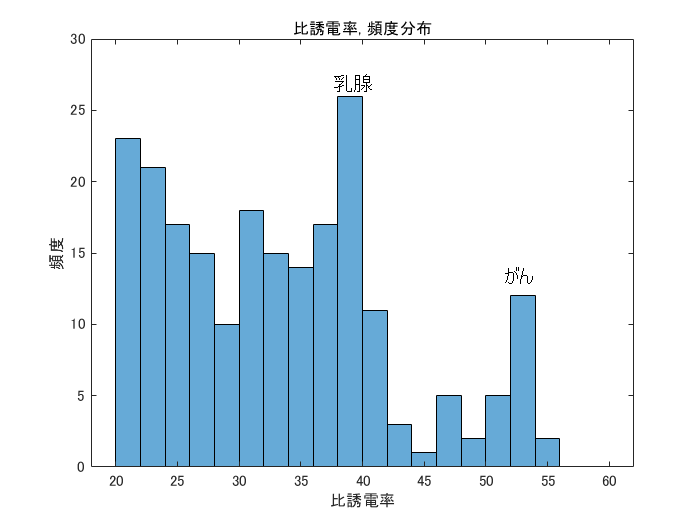
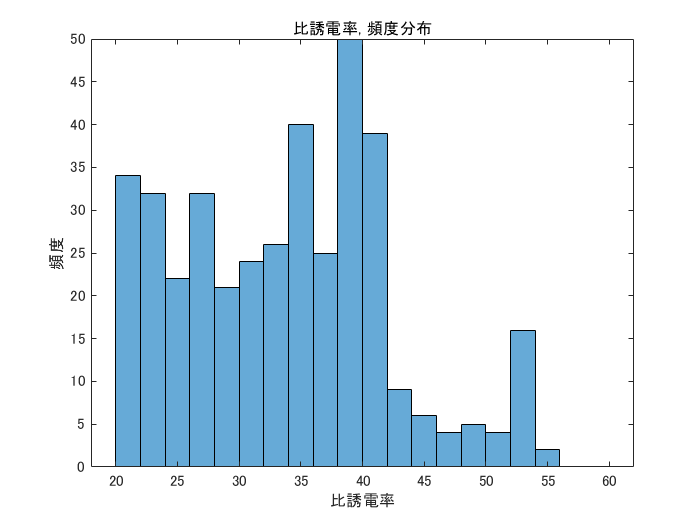
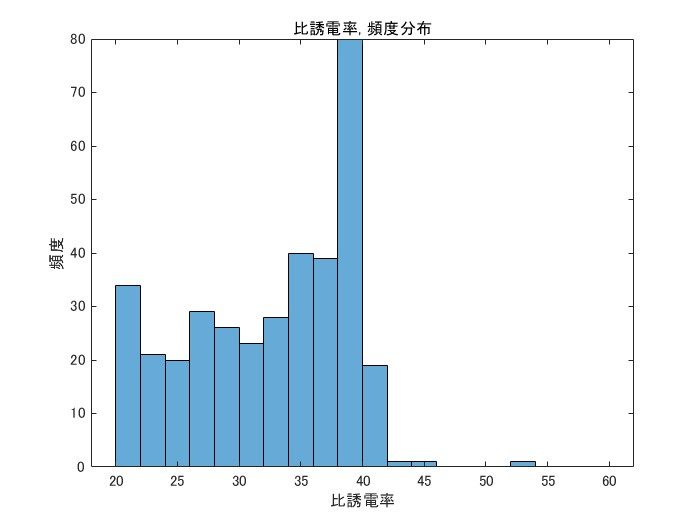
図6-12 比誘電率の頻度分布
(H=5, (nx,ny,nz)=(7,7,4))